The 
error 
on the position measurement
using the five point method,
assuming a Gaussian beam of half-power size 
, and using offsets
of 
, is given by:
or
But it is more efficient to move the antennas so that one out of five is always pointed. Then each pointed antenna is worth 4 displaced ones, in terms of final signal to noise ratio. Thus
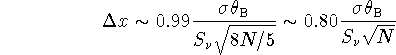
Let us now estimate 
for N antennas of diameter D, at
frequency 
. Assuming a band with of 8 GHz and an integration time
of 
seconds:
then using 
:
Note that the dependence on frequency is to first order only through
the source flux 
, since one may assume 
at
all frequencies.
The actual duration of the pointing measurement can be estimated as
where 
is the angular
distance (in degrees) to find a suitable pointing source. Here I
assume a settling time of 2 seconds between two consecutive points in
the five-point map, and a slewing rate of 1 degree per second.
If we want to be able to point frequently (say every 15 minutes), and
are willing to spend less than 
of the time on pointing, then a
practical upper limit on is 15 seconds; we do not wish to go
further than 
degrees, since a higher value will put
severe constraints on the accuracy on the pointing model.
Then the minimum usable flux is set by:
Values for different array options are given in
Table 2. The pointing goal there is to obtain a rms
pointing error of 
at 300 GHz. Thus we set to
half of this value so that the measurement error does not contribute
significantly to the rms pointing error. This sets the minimum flux;
the density of sources above that minimum flux is estimated from
Holdaway et al. ([1994]). It appears that the 
m may have serious difficulties to find enough pointing sources,
while the proposed large homogeneous arrays should have enough
sensitivity for frequent, high accuracy pointing measurements, thus
relaxing the requirements on pointing stability on time scales longer
than about 30 minutes.
For heterogeneous arrays with 
antennas of sizes 
,
the minimum flux becomes (see Appendix A):
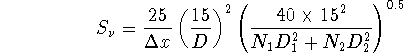
The results in Table 2 are then unchanged if part of the arrays are replaced by antennas of different sizes, provided the total collecting area is conserved. Note that here the need to correlate the smaller antennas with the larger ones is essential.
We have assumed here that the pointing could be calibrated at any frequency. It is of course desirable to calibrate the pointing at the observing frequency. Different aperture illuminations at widely different frequencies combined with time-dependent structural deformations might cause a time variable pointing difference between the two beams. This should be more closely investigated.
Weakest usable pointing calibrator (integration 
s).
The minimum flux does not depend on frequency (assuming
K/GHz), while the source counts apply only at 90
GHz. The last column is the angular radius of the cone in which one
pointing source is to be found on average.
| N | D | | |  | |
| (m) | ('') | (mJy) | (sr  ) | (deg.) | |
| 128 | 8 | 0.53 | 173 | 166 | 2.5 |
| 90 | 10 | 0.43 | 132 | 249 | 2.0 |
| 64 | 12 | 0.35 | 109 | 333 | 1.8 |
| 40 | 15 | 0.28 | 88 | 457 | 1.5 |