Assume we have an interferometer with N antennas. We want to
determine the power gain 
of antenna i, by observing a point
source of flux density S.
The quantities we measure are the baseline amplitudes: Let us note
the amplitude of the correlation product of the outputs of
antennas i and j.
One has:
which may be written, since the power gains are positive:
where 
, and 
.
We thus have N (N-1) linear equations to solve for the N unknowns
. Such a system is usually solved using the method of least squares.
One minimizes:
for which the N conditions are:
which may be rewritten as:
Adding these equations one obtains:
It is then straightforward to substitute this back and get:
Here the second term contains all the baseline amplitudes. This formula is derived in a much more elegant way (and in French) by E. Anterrieu ([1992]). Let's rewrite it in a slightly different way:
Now the first term contains all baselines connected to antenna i, the second one contains all the other baselines; for instance for 3 antennas, one obtains the well-known formula:
Now all the 
contain noise terms which are uncorrelated.
Then for the corresponding r.m.s. fluctuations we get:
In the large signal-to-noise limit: 
,
.
Let us assume further that all antennas have the same gain 
and sensitivity: 
:
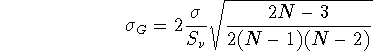
The rms of the power gain
is thus behaving like 
in
the large N limit. This is because in Eq. 1 the first
(N-1) terms are going to dominate the summation when N is large,
since the other (N-1)(N-2)/2 are multiplied by a 
factor. The rms gain also diverges for N <3: it is well-known that
it is not possible to measure the gain of a single antenna in a
two-element interferometer. This formula slightly differs from that of
Cornwell and Fomalont ([1989]); the asymptotic behaviour is
the same ( 
for the amplitude gains)
but their result diverges for N=3.
In the case of heterogeneous arrays the previous analysis has to be refined; We do this in Appendix A. The result for a large number of antennas is simply:
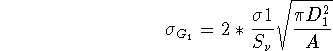
where 
is the gain of kind 1 , 
the rms in one baseline
connecting two antennas of kind 1, and A is the total collecting area
of the array.
