(1) - National Radio Astronomy Observatory, Socorro, New Mexico, USA
L. Kogan![]()
(1) - National Radio Astronomy Observatory, Socorro, New Mexico,
USA
It is shown that the level of negative side lobes in any array beam (PSF - Point Spread Function) is equal ![]() , where N is number of elements at the array. For the central symmetry arrays all negative side lobes are tangent to the horizontal line at the level
, where N is number of elements at the array. For the central symmetry arrays all negative side lobes are tangent to the horizontal line at the level ![]() . For large N positive side lobes are bigger than negative ones (in absolute values). For example, for N = 36 (accepted value for MMA now) the value of negative side lobes is 0.0286. The level of negative side lobes in the natural weighting case does not depend on the array configuration and is determined completely by the number of the elements at the array
. For large N positive side lobes are bigger than negative ones (in absolute values). For example, for N = 36 (accepted value for MMA now) the value of negative side lobes is 0.0286. The level of negative side lobes in the natural weighting case does not depend on the array configuration and is determined completely by the number of the elements at the array
Let's suppose the vector ![]() determines the position of the array element at the aperture of the array measured at wavelengths. Then the beam pattern of the array is determined by all nonzero baselines and can be verified by the following equation in the natural weighting case.
determines the position of the array element at the aperture of the array measured at wavelengths. Then the beam pattern of the array is determined by all nonzero baselines and can be verified by the following equation in the natural weighting case.
whereNow let's calculate the similar double sum including zero baselines.is the vector of the direction on the sky
N is the number of elements in the array.
whereWhat is the difference betweenis a voltage beam pattern.
The level of negative side lobes in the natural weighting case does not depend on the array configuration and is determined completely by the number of the elements at the array
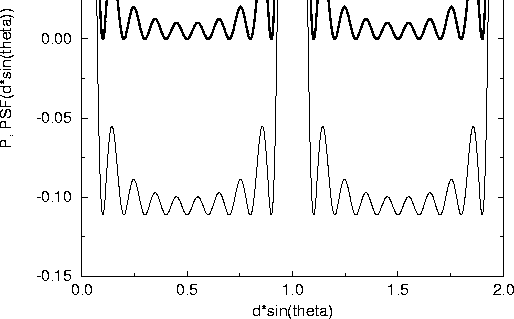
Figure 1: Point spread function PSF![]() and
P
and
P![]() for one dimension homogeneous array of N=10 elemments with spacing d
for one dimension homogeneous array of N=10 elemments with spacing d
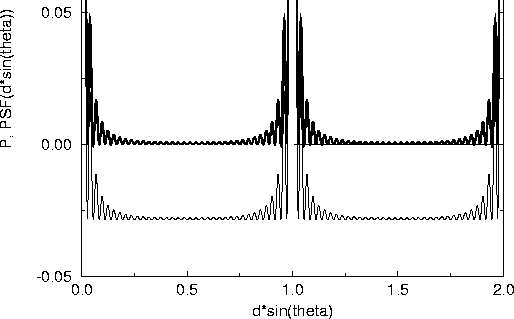
Figure 2: Point spread function PSF![]() and
P
and
P![]() for one dimension homogeneous array of N=36 elements with spacing d
for one dimension homogeneous array of N=36 elements with spacing d