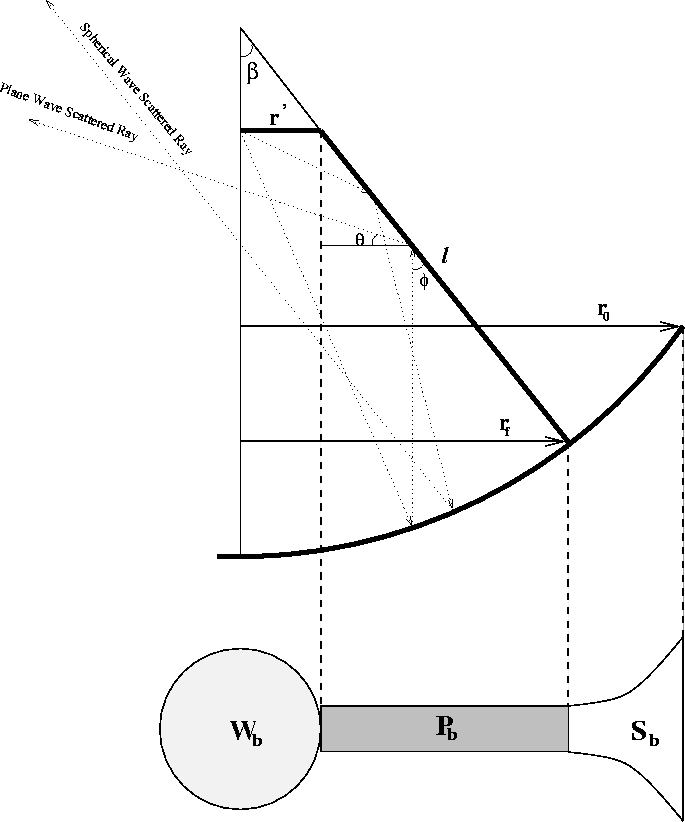
Figure 1: Geometrical definitions used in this memo. The lower
part of the figure shows a geometrical representation of the three
terms which contribute to the aperture blockage.
Jingquan Cheng
email: jcheng@nrao.edu
and
Jeffrey G. Mangum
email: jmangum@nrao.edu
National Radio Astronomy Observatory
949 North Cherry Avenue
Tucson, AZ 85721
This memo analyzes the changes in system temperature and scattered radiation termination location with feed leg attachment position and feed leg geometry. Calculation of the changes in system temperature with feed leg attachment radius shows that there is a relatively small penalty paid when the feed legs are attached inside the reflector surface. A ray tracing analysis of the termination locations for scattered radiation indicates that feed leg attachment to the edge of the antenna may not be the best configuration either from the total blockage point of view or from the spillover noise point of view.
In this discussion, we will use the following definitions (see Figure 1):

Figure 1: Geometrical definitions used in this memo. The lower
part of the figure shows a geometrical representation of the three
terms which contribute to the aperture blockage.
The signal blockage in a Cassegrain system has three terms: blockage of the plane wave due to the central subreflector hub, blockage of the plane wave due to the feed legs, and blockage of the primary surface reflected (spherical) wave due to the feed legs. The form for each of these blockage terms is dependent upon the aperture illumination pattern. We will consider two types of illumination: uniform (Maanders 1975) and tapered gaussian (Lamb 1986). A good general discussion of this problem can be found in Ruze (1968). The voltage distribution function for these types of illumination pattern are given by
where
The blockage due to the subreflector hub is given by
The plane wave blockage due to the feed legs is given by
The spherical wave blockage due to the feed legs is given by
where the Error Function erf(x) is given by
The length of a feed leg is given by (see Figure 1)
In the antenna design, the feed leg stiffness is a very important consideration. The feed leg stiffness is limited by the feed leg width. For a typical rectangular shaped feed leg, the moment of inertia is
The feed leg stiffness under distributed load conditions is represented by
From the above formulae, for a given feed leg stiffness the feed leg width can be reduced in proportion to its change in length. In the following, we apply this relationship in the blockage calculation. However, two effects associated with the feed leg dimensions will not be considered in this memo. The first is that changes in the feed leg support position are coupled to the requirements for the reflector stiffness. For reflector edge feed leg support, the reflector stiffness will be an important factor in reducing the feed leg overall stiffness. The second consideration which we do not address is the fact that we do not take into account the influences of the resonant frequencies of the antenna on the feed leg geometry. For all antenna diameters considered in the memo, the feed legs are assumed to have the same dimensions.
In the following we estimate the effects of blockage to the system temperature for an 8, 10, 12, and 15m diameter telescope with both uniform and tapered gaussian illumination. In Table 1 we list our assumed parameters used in these calculations.
| focal ratio (f) | 0.38 |
|
subreflector diameter ( | |
| feed leg width (w) | |
| feed leg depth (h) | 0.20 m |
|
primary focus to feed leg distance (r |
|
|
number of feed legs ( | 4 |
|
observing frequency ( | 230.0 GHz |
| source elevation (el) | |
|
atmospheric opacity ( | 0.1 |
|
ambient temperature ( | -5.0 C |
|
double sideband receiver temperature ( | |
|
image termination temperature ( | 4.2 K |
|
forward scattering and spillover efficiency ( | 0.73 |
|
minimum blockage 8m blockage efficiency ( | 0.98 |
| minimum blockage 8m rear scattering, spillover | |
|
and ohmic loss efficiency ( | 0.97 |
| fraction of total area blocked for minimum blockage 8m | |
|
( | 2.149 % |
|
( | 2.603 % |
Figures 2 and 3 show the area blocked,
and the contributions from the central hub, plane wave, and spherical
wave to that blockage, as a function of the feed leg attachment
radius ![]() for both uniform and 11dB edge-tapered gaussian illumination
functions. From these figures one sees that the spherical wave
blockage term dominates for
for both uniform and 11dB edge-tapered gaussian illumination
functions. From these figures one sees that the spherical wave
blockage term dominates for ![]() in the
uniform illumination case and for
in the
uniform illumination case and for ![]() in the
11 dB edge tapered case. Beyond these radii the plane wave term
dominates, primarily because of the thicker feed leg necessary.
Comparison of Figures 2 and 3 also
shows that an edge taper minimizes the contribution of the spherical
wave blockage term.
in the
11 dB edge tapered case. Beyond these radii the plane wave term
dominates, primarily because of the thicker feed leg necessary.
Comparison of Figures 2 and 3 also
shows that an edge taper minimizes the contribution of the spherical
wave blockage term.
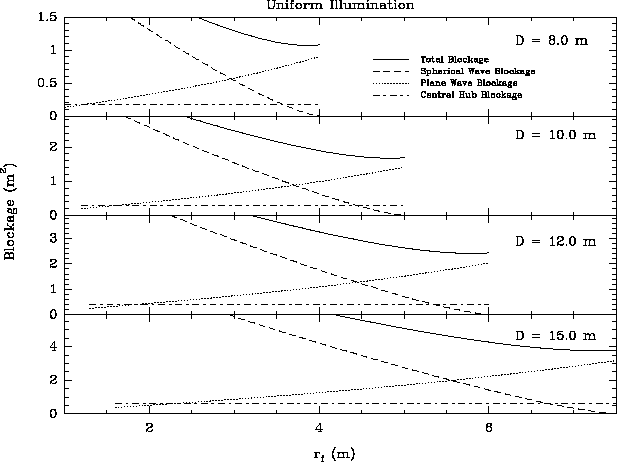
Figure: 2 Total collecting area blocked as a function of the feed leg
attachment radius ![]() assuming a uniform illumination function and
the assumed values given in Table 1.
assuming a uniform illumination function and
the assumed values given in Table 1.
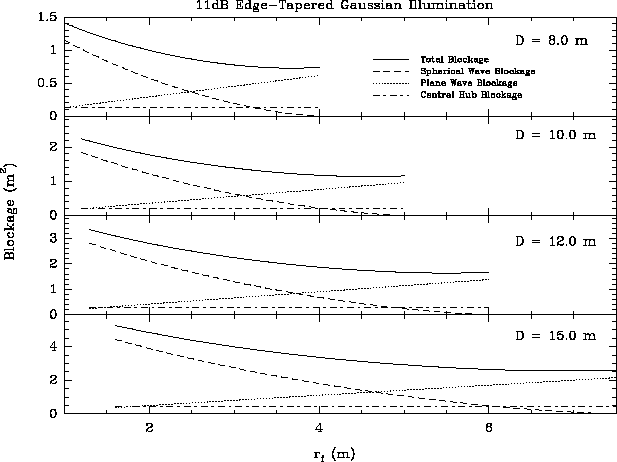
Figure 3: Total collecting area blocked as a function of the feed leg
attachment radius ![]() assuming an 11dB edge-tapered gaussian illumination
function and the assumed values given in Table 1.
assuming an 11dB edge-tapered gaussian illumination
function and the assumed values given in Table 1.
Figure 4 shows the fraction of the total area blocked for D = 8, 10, 12, and 15m for both a uniform and an 11dB edge-tapered gaussian illumination function. Note that the total collecting area is given by
As in Figures 2 and 3, the effects of the edge taper are apparent. Note also that the slight increase in the blocked fraction as the feed leg encounters the edge of the reflector is due to the fact that we have assumed that the feed leg can be made narrower in proportion to its length.
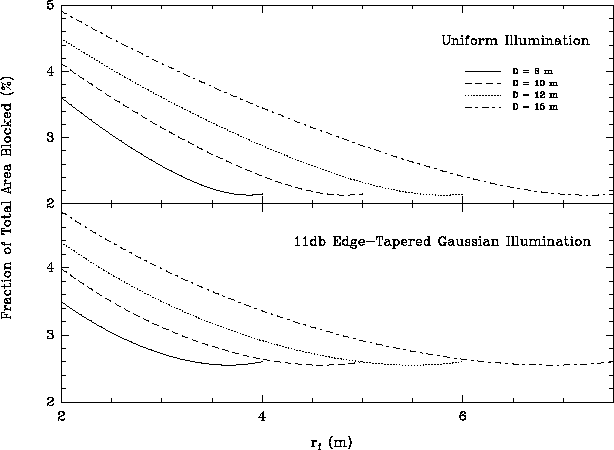
Figure 4: Fraction of total collecting area blocked for both a uniform
and an 11dB tapered gaussian illumination function.
To calculate the system temperature ![]() as a function of feed
leg attachment radius, we use the assumptions listed in Table
1. The SSB system temperature of a single
sideband system on the
as a function of feed
leg attachment radius, we use the assumptions listed in Table
1. The SSB system temperature of a single
sideband system on the ![]() scale (note that we drop the ``*'' in
the following notation for simplicity) is given by the
following equations (see MMA Memo 170 for details)
scale (note that we drop the ``*'' in
the following notation for simplicity) is given by the
following equations (see MMA Memo 170 for details)
The antenna temperature of the sky is given by the sum of noise contributions due to sky, antenna, and cosmic microwave background emission
where
Since as the fractional area blocked increases as the aperture efficiency
decreases, we can calculate the rear scattering and spillover
efficiency as a function of feed leg attachment radius ![]() using
using
where ![]() is the fraction of the total area blocked in
the design under consideration and
is the fraction of the total area blocked in
the design under consideration and ![]() is the rear
scattering and spillover efficiency for the minimum blockage antenna
for a given diameter. We further assume that the efficiencies for the
minimum blockage design for each diameter are the same as that for the
8m diameter MMA design.
is the rear
scattering and spillover efficiency for the minimum blockage antenna
for a given diameter. We further assume that the efficiencies for the
minimum blockage design for each diameter are the same as that for the
8m diameter MMA design.
Figure 5 shows the system temperature ![]() as
a function of the feed leg attachment radius
as
a function of the feed leg attachment radius ![]() using the
assumptions listed in Table 1. As expected,
attaching the feed legs near the edge of the antenna reflector
produces the lowest amount of ground pickup. The penalty for moving
the feed legs inward, though, is quite small.
using the
assumptions listed in Table 1. As expected,
attaching the feed legs near the edge of the antenna reflector
produces the lowest amount of ground pickup. The penalty for moving
the feed legs inward, though, is quite small.
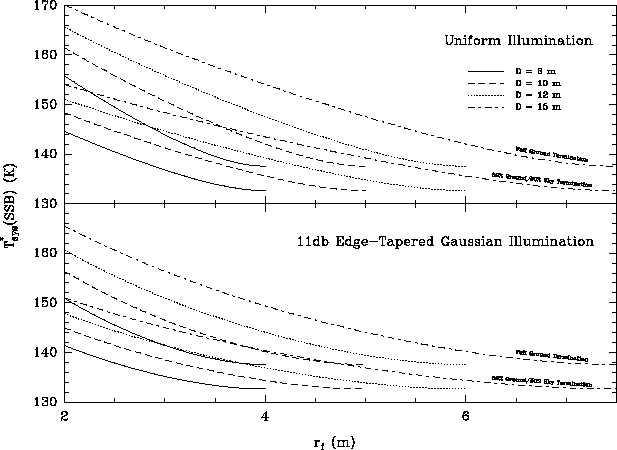
Figure: 5 ![]() as a function of
as a function of ![]() using the assumptions listed
in Table 1. Note also that we assume that the
efficiency for the minimum blockage design for each diameter
(
using the assumptions listed
in Table 1. Note also that we assume that the
efficiency for the minimum blockage design for each diameter
(![]() ) is the same as that for the 8m diameter MMA design.
Two cases of spillover radiation are shown. The darker lines for each
diameter represent the case where all of the scattered radiation
terminates on warm ground. The lighter lines for each diameter
represent the case where 50% of the radiation terminates to cold sky
and 50% to warm ground.
) is the same as that for the 8m diameter MMA design.
Two cases of spillover radiation are shown. The darker lines for each
diameter represent the case where all of the scattered radiation
terminates on warm ground. The lighter lines for each diameter
represent the case where 50% of the radiation terminates to cold sky
and 50% to warm ground.
Two cases for the termination point of the scattered radiation are shown in Figure 5. The worst-case scenario (``Full Ground Termination'' in Figure 5), where all of the scattered radiation terminates to warm ground, can easily be avoided. In the following, we describe how an appropriate choice of feed leg geometry can improve the scattering properties of a feed leg. An example of how this improvement translates to a reduced system temperature for a given attachment radius is shown in Figure 5 as the case where 50% of the scattered radiation terminates to warm ground and 50% terminates to cold sky.
In the following, we discuss the scattering of radiation from the traditional rectangular feed leg. Following this analysis, we consider the effects of shaping or baffling of feed legs to minimize ground radiation pickup.
In the previous section, the assumption is that all of the scattered radiation is terminated on the warm ground, which is the worst-case scenario. To understand the scattering of radiation due to feed legs at millimeter wavelengths, ray tracing is necessary. Referring to the feed leg geometry shown in Figure 1, if we trace rays from the center of the aperture, the rays will hit the secondary. After reflecting from the secondary, some rays blocked by the feed leg may reach the primary reflector first. These are called plane wave scattering rays. The other rays may reach the feed leg first. These are called spherical wave scattering rays.
The termination point for scattered radiation is a function of the
feed leg geometry. Given the feed leg support radius ![]() , the feed leg
angle with the reflector axis will be:
, the feed leg
angle with the reflector axis will be:
![]()
By taking ![]() , and
, and ![]() the
the ![]() angle
will be:
angle
will be:
![]()
Plane wave rays will have a direction parallel to the reflector axis after
reflection from the primary reflector. The simple Snell law will give the
direction of the reflected rays after the feed leg reflection. Taking
![]() as the angle of the reflected rays from the feed leg with the
reflector axis (see Figure 1),
as the angle of the reflected rays from the feed leg with the
reflector axis (see Figure 1), ![]() will be:
will be:
![]()
If we use the angle of the reflected ray above the aperture plane ![]() to represent the scattering direction, then
to represent the scattering direction, then ![]() (see
Figure 1). Negative or smaller
(see
Figure 1). Negative or smaller ![]() angles
represent ground pickup at most observing directions. A higher
angles
represent ground pickup at most observing directions. A higher
![]() angle represents no or little ground pickup at most observing
directions.
angle represents no or little ground pickup at most observing
directions.
Figure 6 shows the ![]() and
and ![]() angles of
the feed leg as a function of
angles of
the feed leg as a function of ![]() . Note that
. Note that
![]() using the scaling law for
using the scaling law for ![]() given in Table 1. From Figure
6, the
given in Table 1. From Figure
6, the ![]() angle increases from
angle increases from ![]() to about
to about ![]() as the
feed leg support radius increases, while the
as the
feed leg support radius increases, while the ![]() angle reduces
greatly from
angle reduces
greatly from ![]() to a negative number. This figure considers
only feed leg reflection and does not take into account what happens
after reflection off of a feed leg. Interception of the scattered
rays begins to occur for
to a negative number. This figure considers
only feed leg reflection and does not take into account what happens
after reflection off of a feed leg. Interception of the scattered
rays begins to occur for ![]() (which corresponds to
(which corresponds to
![]() ). Full interception of the scattered radiation by
the reflector occurs at the
). Full interception of the scattered radiation by
the reflector occurs at the ![]() angle of:
angle of:
![]()
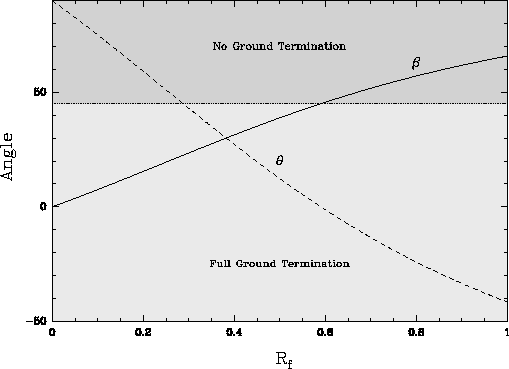
Figure 6: ![]() and
and ![]() as a function of
as a function of ![]() . For
. For ![]() most scattered radiation terminates to warm ground, while for
most scattered radiation terminates to warm ground, while for
![]() most scattered radiation terminates to cold sky. The ``No
Ground Termination'' and ``Full Ground Termination'' regions are drawn
assuming an elevation angle of
most scattered radiation terminates to cold sky. The ``No
Ground Termination'' and ``Full Ground Termination'' regions are drawn
assuming an elevation angle of ![]() .
.
Inserting Equation 1, the full-interception ![]() angle
occurs for
angle
occurs for ![]() . After hitting the reflector again,
the scattering rays will reflect above the aperture plane or hit the
reflector a third time and end up terminated on cold sky.
Spherical wave rays reflect off of the feed legs at very small incident
angles, so will always fall on the reflector surface. Therefore the
terminations of these rays should be high above the aperture plane.
. After hitting the reflector again,
the scattering rays will reflect above the aperture plane or hit the
reflector a third time and end up terminated on cold sky.
Spherical wave rays reflect off of the feed legs at very small incident
angles, so will always fall on the reflector surface. Therefore the
terminations of these rays should be high above the aperture plane.
For a thorough understanding of feed leg scattering, a ray tracing
program has been written to analyze the problem. The program starts
the ray tracing from the receiver horn.
After the ray reaches the secondary mirror, the program follows the
ray tracing to either the main reflector or the feed leg. Further ray
tracing could be done either between these two reflecting surfaces or
within the primary reflector itself. The ray reflected from the feed leg or
primary mirror to the secondary mirror is not considered (the
secondary mirror is small, so the effect is not significant). The ray
tracing is done for different feed leg support radii ![]() . After
running this program, the resultant ray termination is shown in
Figure 7.
. After
running this program, the resultant ray termination is shown in
Figure 7.
Figure 7 shows the rectangular shaped feed leg
scattering ray termination angle for different feed leg support
radii. From this figure one can see that there are four
groups of curves. The horizontal lines in ![]() shown as Region A
represent reflected radiation off of a feed leg. The continuation of
these reflected rays is shown as Region B, which represents reflection
from feed leg to antenna to sky. As the feed leg support radius
shown as Region A
represent reflected radiation off of a feed leg. The continuation of
these reflected rays is shown as Region B, which represents reflection
from feed leg to antenna to sky. As the feed leg support radius ![]() increases, the scattering ray angles above the aperture plane (
increases, the scattering ray angles above the aperture plane (![]() )
are reduced. When
)
are reduced. When ![]() is 0.8,
is 0.8, ![]() is negative, so that all
scattered radiation hits the ground directly, producing noise in the
system as predicted.
is negative, so that all
scattered radiation hits the ground directly, producing noise in the
system as predicted.
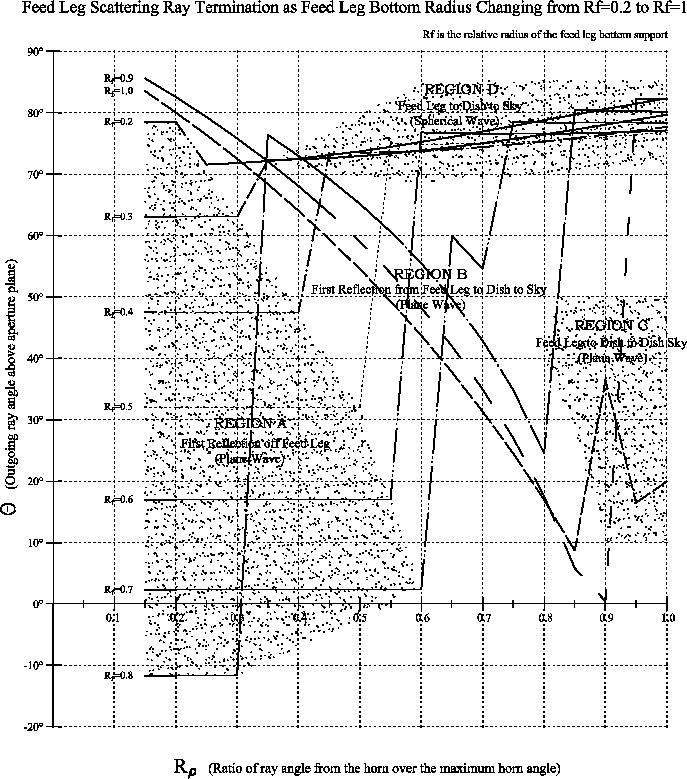
Figure 7: Ray tracing results. Four regions, representing four types
of reflection from the feed legs and surface of the antenna, are indicated.
Region B and C in Figure 7 represents plane wave
scattered radiation intercepted by the reflector twice, or three
times. Curves in Region B run from the top left down to the bottom
right of the figure. The curve for ![]() in Region C is a ray
which reflects three times off of the reflector surface. The last
region in Figure
7, Region D, represents the spherical wave
scattering. As we predicted before, this scattered radiation always
terminates to cold sky.
in Region C is a ray
which reflects three times off of the reflector surface. The last
region in Figure
7, Region D, represents the spherical wave
scattering. As we predicted before, this scattered radiation always
terminates to cold sky.
>From this figure, one could find that the feed leg reflector edge support produces not a best solution for the antenna design from the ground noise pickup point of view. However moving the feed leg inwards may produce lower plane wave scattering. This will be discussed in the following section.
In the past, Moreira , Satoh , and Lawrence had extensive study on the issue of the ground spillover pickup and feed leg shaping or baffling. The ground spillover pickup by the feed leg could be greatly reduced either by shaping the feed leg, by adding a dielectric layer to the surface of the feed leg, or by adding baffles over the feed leg surfaces. These analyses are done by wave theory and existing examples are available only for relatively low frequency ranges (4-50 GHz).
One shaping technique is to attach a triangular roof on the inner side
of the feed leg (Lamb 1998). By geometrical optics, if the half angle
of the roof is ![]() , then the reflected rays from these tapered
feed legs will have:
, then the reflected rays from these tapered
feed legs will have:
By adjusting the roof half angle, the scattering rays of the feed leg could
all be terminated to cold sky independent of their incident angle on
the feed leg. This is also the finding made by Lamb. Figure
8 shows Equation 20 as a function of
![]() for representative values of
for representative values of ![]() .
.
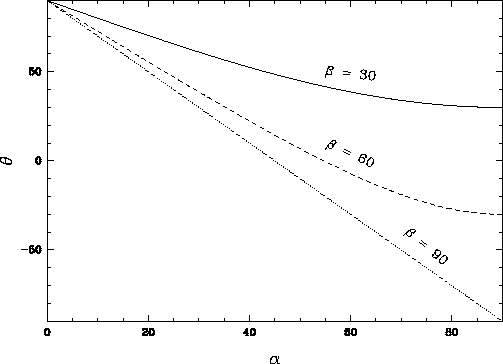
Figure 8: The scattered ray angle relative to the aperture plane
![]() as a function of the feed leg taper angle
as a function of the feed leg taper angle ![]() for feed
leg to reflector axis angles
for feed
leg to reflector axis angles ![]() of 30, 60, and 90
of 30, 60, and 90![]() .
.
The roof angle of the feed leg will reflect the spherical rays from the secondary mirror outwards in radius. This makes the incident angle on the primary mirror reflection approach the incident angle of ray, which will cause the ray to hit the same location of the reflector if the feed leg is removed. Therefore, the spherical scattering rays will go even higher above the aperture plane as shown in Lamb (1998). Note also that the shaped feed leg will produce an angle change in the azimuth direction. This has little effect on the noise pickup.
Jewell, P. R. and Mangum, J. G., 1997, ``System Temperatures, Single Versus Double Sideband Operation, and Optimum Receiver Performance'', MMA Memo 170. Lamb, J. W., 1998, Spillover Control on Secondary Mirror Support Struts, Internal Memo. Lamb, J. W. & Olver, A. D., 1986, IEE Proceedings, 133, 43. Lawrence, C. R., Herbig, T., & Readhead, A. C. S., 1994, Reduction of Ground Spillover in the Owens Valley 5.5m Telescope, IEEE Proc. 82, 763-767. Maanders, E. J., 1975, ``Enige Aspecten van Grondstation Antennes voor Satelliet Communicatie'', Dissertation, State University of Gent, Belgium. Moreira, F. J. S., Prata, A., & Thorburn, M. A., 1996, ``Minumization of the Plane-Wave Scattering Contribution of Inverted-Y Strut Tripods to the Noise Temperature of Reflector Antennas'', IEEE Trans AP-44, 492. Ruze, J., 1968, Microwave Journal, 11, 76. Satoh, T., Endo, S., Matsunaka, N., Betsudan, S., Katagi, T., & Ebisui, T., 1984, ``Sidelobe Level Reduction by Improvement of Strut Shape'', IEEE AP-32, 698.