where
is the density of liquid water (
g/cm
).
The amount of water vapor in the atmosphere above the VLA is an interesting quantity for two reasons: water vapor contributes significantly to the opacity of the atmosphere, and the fluctuations in water vapor are the dominant source of interferometric phase fluctuations. We currently have the capability to constantly monitor the phase stability of the atmosphere, with the site-testing interferometer (Carilli & Roy 1998), and we also have the capability to directly measure the opacity in any of the observing frequency bands of the VLA, with the array antennas themselves (through TIP scans - Butler 1996). However, TIP scans are done at essentially random frequency bands and times. Also, the site-testing interferometer has only been operating for a short time, so information over long time periods is not available from that instrument. If information on atmospheric water were available, then it could be used with atmospheric models to produce estimates of opacity quite reliably. The estimation of phase stability from total water is considerably less certain. Although it is generally true that more water vapor means more unstable phase conditions, this is not always strictly true. In the ideal case, it is desirable to know the full vertical distribution of water vapor in the atmosphere, but this is a quantity which is not easy to measure (it can be done with a variety of techniques, but we have no such capability at the VLA). However, even some crude indicator of the total amount of water vapor in the atmosphere is better than nothing. The total column of water is just such a beast. This is the equivalent depth of water which would result if all of the water vapor in the atmosphere were concentrated into a layer of liquid. It is also commonly referred to as the amount of precipitable water. While knowing the precipitable water yields little information regarding the phase fluctuations, it can be used to make a first order prediction of the opacity of the atmosphere.
Given measurements of surface temperature and dew point, a rough estimate of the precipitable water can be made. Uncertainties in the actual profile of water vapor make this a truly rough estimate, but it is probably good to a few 10's of %. Such measurements are available from the electronic versions of the observing logs which have been made for some time now. The logs from mid-1990 up to the present are currently available, so this is the time period that will be presented in this memo.
Consider a column of liquid water with cross-sectional area A, and
height h. This height (h) is the precipitable water. The mass of
this column of liquid water is:
where is the density of liquid water ( g/cm).
Now, the mass of the water vapor in an atmospheric column with
cross-sectional area A is:
where 
is the mass of each water molecule (
amu), 
is the number density of water molecules, and the integration is done
over altitude z. This integration over altitude is why it is
strictly necessary to have the full vertical distribution of water
vapor in order to calculate the precipitable water. However, if the
water vapor is distributed exponentially (similar to the bulk of the
lower atmosphere) like:
where 
is the number density of water vapor at 
(the surface,
practically speaking), and H is the scale height of the water
vapor distribution (the e-folding distance), then the integral can be
done analytically, resulting in:
To find the precipitable water, equate the mass of the vapor to that of
the liquid (conservation of mass):
therefore,
So, given a measurement of , and an estimate for H, the
precipitable water can be estimated. From the ideal gas law, the
number density of water molecules is related to the water vapor partial
pressure (
) and the temperature (
) via:
Making this substitution, the precipitable water is then:
The surface temperature, is measured and recorded regularly in
the observing logs. In fact, it is measured and recorded on the
visibility archive tapes as well, but getting at that data is
logistically harder, and the accuracy and time resolution gain is not
really needed. The surface water vapor partial pressure can be
derived from the surface dew point (D) via (Clark 1987):
where the dew point is in degrees C, and is in millibar. The dew
point is also measured and recorded regularly in the observing logs.
Again, electronic versions of these logs exist, and these can be parsed
for the temperature and dew point quantities.
What to use for the scale height H? Formally, for an isothermal
atmosphere in hydrostatic equilibrium the scale height is given by:
where g is the gravitational acceleration. If this were the right
value for H, then substituting this would yield the following very
simple equation for the precipitable water:
Unfortunately, it turns out that the above formal expression for the
scale height is not correct for water vapor. Given a typical surface
temperature (
C), that expression would give a scale
height of about 13 km. Observationally, the scale height of water
vapor in the Earth's atmosphere is between 1.5 and 2 km (e.g. Ulich
1980). Therefore, the slightly more complicated expression (with scale
height and surface temperature explicitly included) must be used. In
this memo, a scale height of 1.5 km will be assumed. Since the derived
precipitable water is linearly proportional to the assumed scale
height, the results can be scaled as desired with little effort.
Electronic versions of the observers logs from the beginning of September 1990 through the end of August 1998 were parsed for recorded values of temperature and dew point. Oddball values were excluded (quite often, for example, the dew point and temperature would be switched, or the dew point would not have a negative sign when it clearly should have). A total of 26659 valid combinations of temperature and dew point were found and used. The values were used to calculate the precipitable water (h) according to the above formula, and this value along with the date and time were recorded for analysis. Figure 1 shows a plot of the entire set of data obtained. The seasonal variation is readily apparent in the data. Figure 2 shows the data for 1997 only. The effects of weather systems can be seen clearly at this higher time resolution (variations on the scales of a few to 10 days).
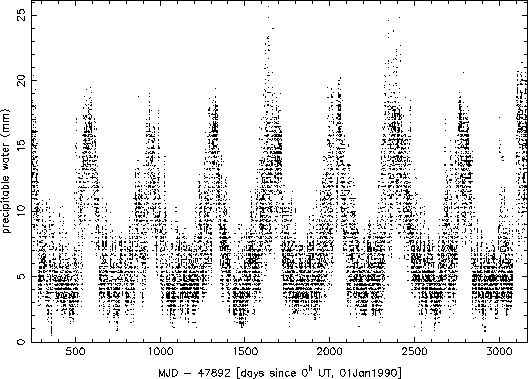
Figure 1: All precipitable water data from September 1, 1990 to August
31, 1998.
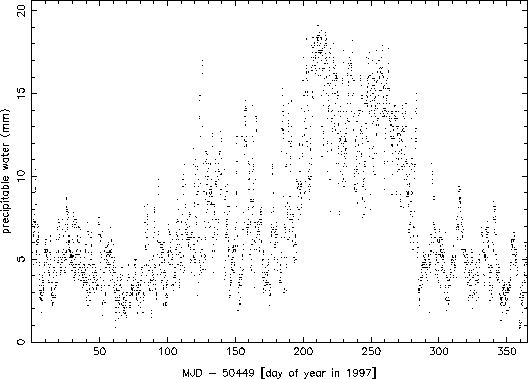
Figure 2: Precipitable water data for 1997.
Figure 3 shows the monthly mean and minimum value (the absolute lowest value in all of the data for that month) for all of the data. Again, the seasonal variation is clearly evident. The wet summer months have a mean precipitable water which is more than twice what it is in the winter months. The typical mean precipitable water in the ``winter'' months (November - April) is about 5 mm, while in the middle of ``monsoon'' season (July and August), the typical mean precipitable water is as bad as almost 15 mm. The absolute very best conditions are about 1 mm of precipitable water in the months from December to April, about 2 mm in October, November, May, and June, about 3 mm in July and September, and about 6 mm in August.
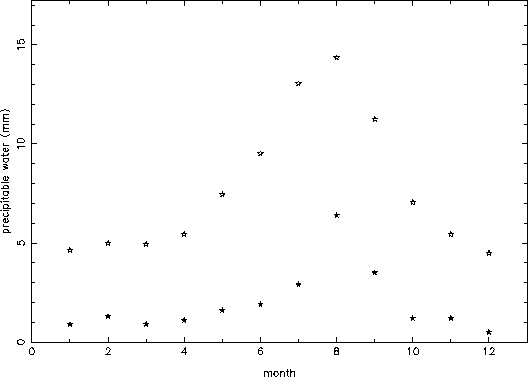
Figure 3: Monthly mean (open stars) and absolute minimum (filled stars)
values of precipitable water.
Figure 4 shows the hourly mean values for all of the data. No clear trend is apparent, which is somewhat surprising on first inspection. However, when looking at the winter data by itself, a clear diurnal variation of about 20% is seen (Figure 5). This must be because during winter night, a sizable portion of the atmospheric water freezes out, lowering the amount of vapor. During the summer, on the other hand, the atmosphere does not cool down enough to freeze out an appreciable fraction of the vapor, and so little diurnal variation is seen. Since the summer precipitable water values are larger than the winter ones, they mask the wintertime signature in the overall average.
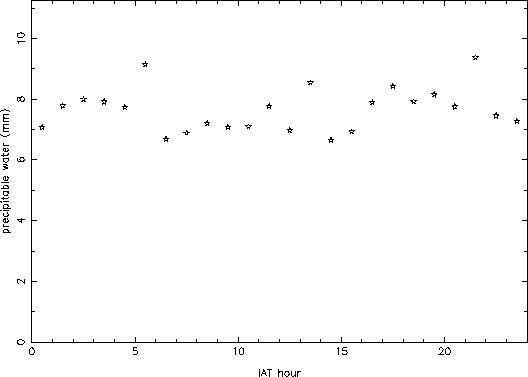
Figure 4: Hourly mean values of precipitable water.
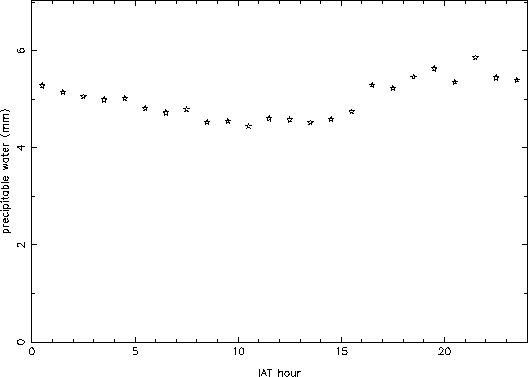
Figure 5: Hourly mean values for wintertime data only (November through
April).
Since water vapor is one of the primary contributors to the opacity
at radio wavelengths, the opacity is expected to correlate very well
with the amount of precipitable water. However, there is some
disagreement about whether surface measurements can yield any
reasonable estimate of the precipitable water (e.g. Reber & Swope
1972). In order to test whether the precipitable water derived via the
technique outlined above has a good correlation with true opacity, I
took the results of reliable TIP data taken at K-band (frequencies
between about 21 and 25 GHz) over the last 3 years (177 TIP scans in
total), and plotted the measured opacity (via the technique outlined in
Butler 1996) against the estimated precipitable water (via the
technique outlined above - the temperature and dew point are provided
with each set of TIP data). The result is shown in Figure 6. A good
correlation is seen, and a fit with a second order polynomial is also
shown in Figure 6. This fit is of the type:
where the three coefficients are: 
= 3.8%, 
= 0.23%,
= 0.065%. While individual data points can be significantly
different from the fit, for the purposes of statistical analysis it
seems quite valid to use the surface measurements to predict
precipitable water (and hence opacity).
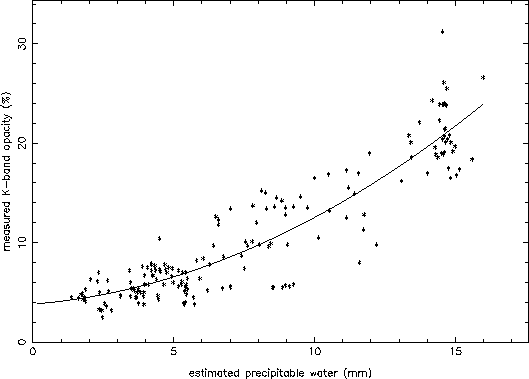
Figure 6: Measured opacity at K-band at the VLA (via TIP scans) compared
with estimated precipitable water over the past 3 years.
Is this correlation unique to K-band, the VLA band where the opacity
effects of atmospheric water are greatest? In order to test this, I
took TIP data at Q-band (I used data only from frequencies between 42
and 44 GHz) from the same 3 year period (164 TIP scans in total), and
plotted the same quantities (measured opacity against estimated
precipitable water). The result is shown in Figure 7. Again, a good
correlation is seen. The fit coefficients are: = 5.5%,
= 0.19%, and = 0.0026%.
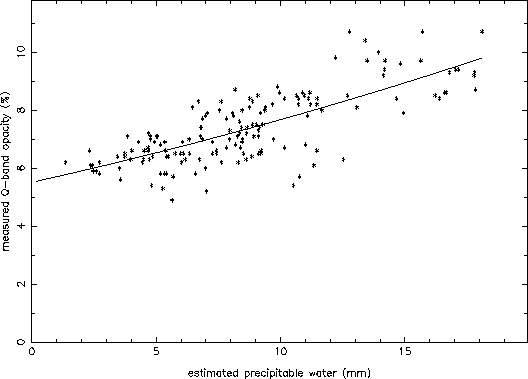
Figure 7: Measured opacity at Q-band at the VLA (via TIP scans) compared
with estimated precipitable water over the past 3 years.
Thanks to Phillip Hicks, Bill Ketzeback, and Tony Perreault for helping with the retrieval of the text versions of the observing logs. Also, thanks to Bill Sahr for keeping me informed whenever new TIP data is taken and downloaded.
Butler, B., Tipping Considerations at the VLA, VLA Scientific Memo No. 170, 1996
Carilli, C., and A. Roy, Calibrating the Site Testing Interferometer, VLA Test Memo No. 213, 1998
Clark, B., Precision of Meteorological Measurements, VLA Scientific Memo No. 158, 1987
Reber, E.E., and J.R. Swope, On the Correlation of the Total Precipitable Water in a Vertical Column and Absolute Humidity at the Surface, J. Appl. Met., 11, 1322-1325, 1972
Ulich, B.L., Improved Correction for Millimeter-Wavelength
Atmospheric Attenuation, Astrophys. Lett., 21, 21-28, 1980