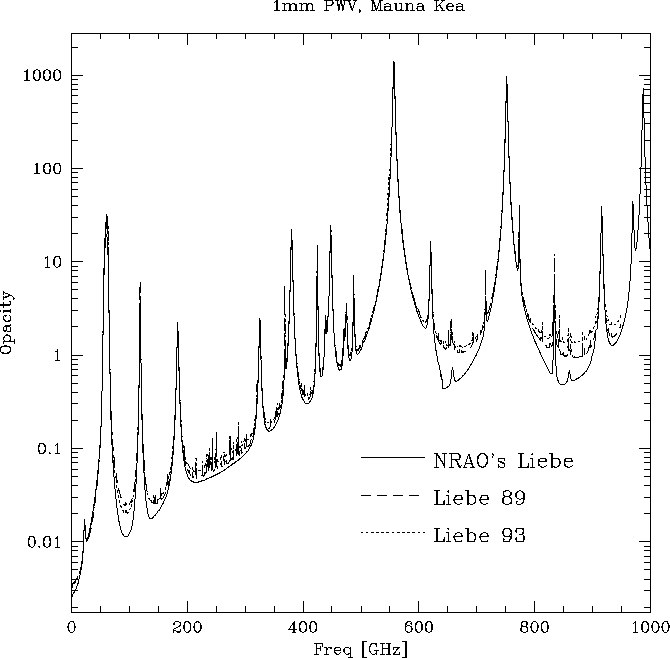
Figure 1: Opacity as a function of frequency with 1 mm PWV above Mauna Kea, for NRAO's Liebe model and the two Liebe models in ATM. In all models, the water vapor was distributed in an exponential profile with 2 km scale height.
M.A. Holdaway
National Radio Astronomy Observatory
949 N. Cherry Ave.
Tucson, AZ 85721-0655
email: mholdawa@nrao.edu
Juan R. Pardo
NASA Goddard Institute for Space Studies
2880 Broadway
New York, NY 10025
email: jpardo@giss.nasa.gov
and
DEMIRM Observatoire de Paris
61 Avenue de l'Observatoire
75014 Paris. FRANCE
Oct 17, 1997
We have found two errors in NRAO's version of the Liebe 1989 atmospheric transmission model. These errors resulted in opacities at the Chajnantor site in the 650 and 850 GHz windows which were a factor of two lower than the corrected model or the Liebe 1993 predict. However, the Hills data set of 225 and 692 GHz opacities from Mauna Kea agrees with the old, buggy NRAO version of Liebe 1989, and not with any models which we now believe to be correct. This ambiguous situation requires more data from the Chajnantor site, but we should also be prepared for higher submillimeter opacities than those in the MMA project had been suggesting. Even so, Chajnantor should be a much better submillimeter site than Mauna Kea, due to the lower precipitable water vapor as inferred from the 225 GHz opacities.
The atmospheric opacity is particularly important in estimating the fraction of the time observations can be made at a given frequency, and what the system temperature and telescope sensitivity will be. To quantify the opacity at what was once perceived as the MMA's workhorse frequency, the NRAO built the 225 GHz site testing radiometers. Now, we are looking toward much higher frequencies, all the way up to 900 GHz. Again, the obvious step to take is to measure the opacity in the submillimeter windows with a tipper or with a Fourier transform spectrometer (FTS), both of which are under way (see, for example Chamberlin et al 1997, Serabyn et al 1997). We can also combine our extensive opacity data at 225 GHz with an atmospheric transmission model to estimate the opacity at other frequencies of interest. NRAO has used a private version of Liebe's millimeter transmission model MPM (described in Liebe, 1989) to estimate the opacity at millimeter and submillimeter wavelengths (Schwab and Hogg, 1988, 1989; and numerous private MMA communications). However, the results from this model seem to be unrealistically optimistic in the submillimeter windows. Yet there are measured submillimeter data from Mauna Kea taken by Richard Hills which support our optimistic model. In this memo, we compare NRAO's version of Liebe 89 with Pardo & Cernicharo's ATM transmission code. Several defects in the NRAO version of Liebe's model have been revealed. Correcting them results in a less optimistic model in the submillimeter, but one which no longer agrees with the Hill's data.
In the late 80's, a copy of Liebe's transmission model was obtained by Harry Lehto for transmission modeling at Green Bank. The numerical coefficients for the various atmospheric lines have been found to be somewhere between the published Liebe 1989 and Liebe 1993 models. A front end to Liebe's model was written to allow input of water vapor, temperature, and pressure profiles from radiosonde data, and the absorption through multiple slabs of atmosphere was calculated with Liebe's model and then integrated. The integration could be performed from any desired site elevation upward. At some point, Fred Schwab came to look after NRAO's version of the Liebe transmission code.
As the frequency range of the MMA grew to encompass the submillimeter, more and more pressure was put on NRAO's version of the Liebe model, though we really didn't realize it. In July 1997, we were able to perform a detailed comparison between the NRAO version of the Liebe model and the Liebe 1989 and Liebe 1993 models in the ATM package (Pardo, 1996). The initial comparison found that NRAO's version of the Liebe model disagreed markedly with either of ATM's Liebe models. Figure 1 shows the disagreement for the case of the Mauna Kea site with 1 mm PWV. The ATM models also have minor atmospheric absorption lines added, while NRAO's model does not. However, the bizarre shape of the submillimeter windows according to NRAO's Liebe model is striking.

Figure 1: Opacity as a function of frequency with 1 mm PWV above Mauna Kea,
for NRAO's Liebe model and the two Liebe models in ATM.
In all models, the water vapor was distributed in an exponential
profile with 2 km scale height.
We found two problems in NRAO's Liebe model which have a minor effect on the millimeter opacity at typical sites, but a profound effect on the submillimeter opacity at extraordinary sites. After correcting these two problems, NRAO's model agreed very well with the ATM Liebe 89 in the submillimeter windows.
Liebe (1993) includes a plot of the opacity through a 1 km horizontal
path of moist air at sea level. We compared the results of NRAO's Liebe
model and ATM's Liebe 89 and Liebe 93 models with Liebe's published
plot and found a defect in the NRAO Liebe model. Figure 2
shows discontinuities about 135 GHz upwards from the 557 GHz and 752 GHz
water vapor lines. Inspection of the code revealed that the line
shape was truncated on the high frequency side at 40 ![]() above
the line frequency. The parameter
above
the line frequency. The parameter ![]() is a measure of the pressure
broadening, so high altitude atmospheric layers would have smaller values
of
is a measure of the pressure
broadening, so high altitude atmospheric layers would have smaller values
of ![]() , which moved the cutoff to lower frequencies, opening up the
submillimeter windows substantially. Because NRAO's Liebe model usually
integrates through several atmospheric slabs with different elevations and
pressures, the discontinuities were largely smoothed over,
resulting in transmission or opacity profiles which did not look as obviously
wrong as Figure 2 indicates. There was an interim report
from Liebe which mentioned the 40
, which moved the cutoff to lower frequencies, opening up the
submillimeter windows substantially. Because NRAO's Liebe model usually
integrates through several atmospheric slabs with different elevations and
pressures, the discontinuities were largely smoothed over,
resulting in transmission or opacity profiles which did not look as obviously
wrong as Figure 2 indicates. There was an interim report
from Liebe which mentioned the 40 ![]() line shape cutoff, but it is
obviously not in the final Liebe 1989 and Liebe 1993 models. After removing
the cutoff from the code, the resulting test opacity profile looks much better
and agrees with the published plot for Liebe's 1989 model (Liebe, 1993).
(see Figure 3).
line shape cutoff, but it is
obviously not in the final Liebe 1989 and Liebe 1993 models. After removing
the cutoff from the code, the resulting test opacity profile looks much better
and agrees with the published plot for Liebe's 1989 model (Liebe, 1993).
(see Figure 3).
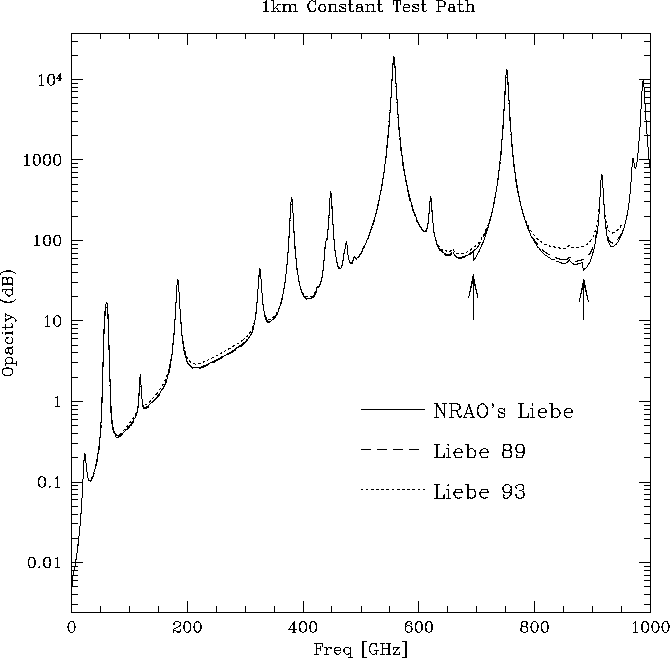
Figure 2: Opacity as a function of frequency for a 1 km horizontal
test path through moist air. The plot is in dB for easy
comparison with Liebe 1993. NRAO's version of the Liebe model
suffers from a nonphysical cutoff in the line shape of the
water vapor lines. Minor lines have been removed to more clearly
identify problems.
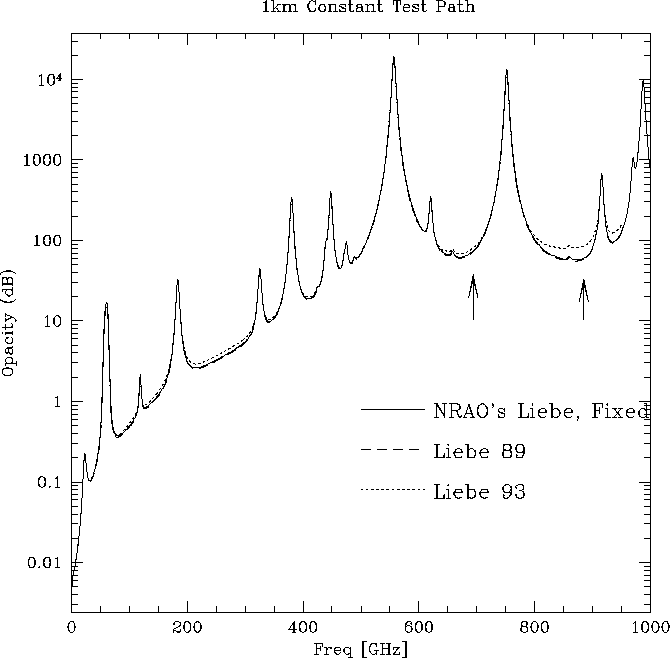
Figure 3: Opacity as a function of frequency for a 1 km horizontal
test path through moist air, after correcting for the
nonphysical line shape cutoff.
The second error we found in NRAO's version of the Liebe model was an error in converting the measured relative humidity into water vapor density. Figure 4 shows the opacity for a 1 km horizontal test path through totally dry air. Even though we edited a fake radiosonde file to indicate 0.00 relative humidity, the code was inserting a small amount of water vapor. This error was traced to the relative humidity conversion, which assumed any dew point below some nominal value was not realistic, and the dew point was set to that nominal value. The radiosonde data usually extends to elevations of about 15 km, and the dew point would dip below the assumed minimum realistic value at about 8 km. Hence, between 8 and 15 km, water vapor was added to the radiosonde data. This extra water vapor was included in the total PWV calculation, but since it was at the highest altitudes and the lowest pressures, it did not suffer from much pressure broadening, and hence did not contribute much to the opacity in the submillimeter windows. Figure 5 shows the opacity for a 1 km horizontal dry test path after the error had been corrected.
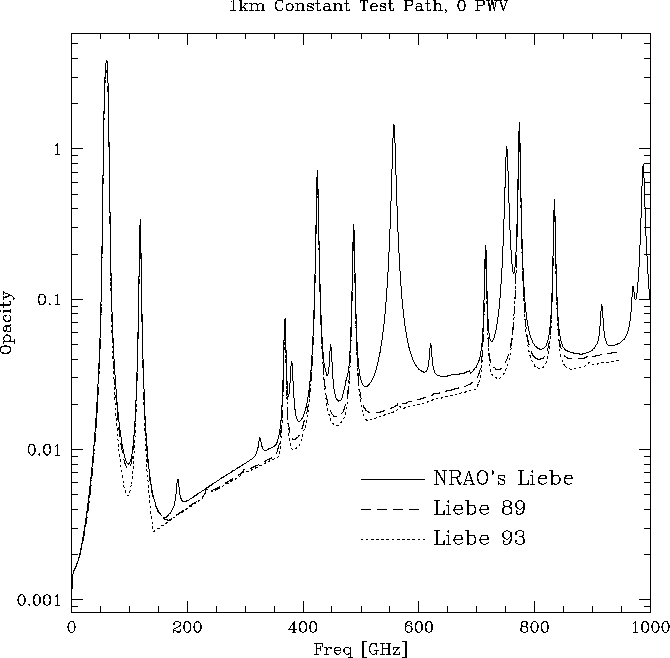
Figure 4: Opacity as a function of frequency for a 1 km horizontal
test path through completely dry air. NRAO's version of the Liebe
model falsely inserts water vapor anyway.
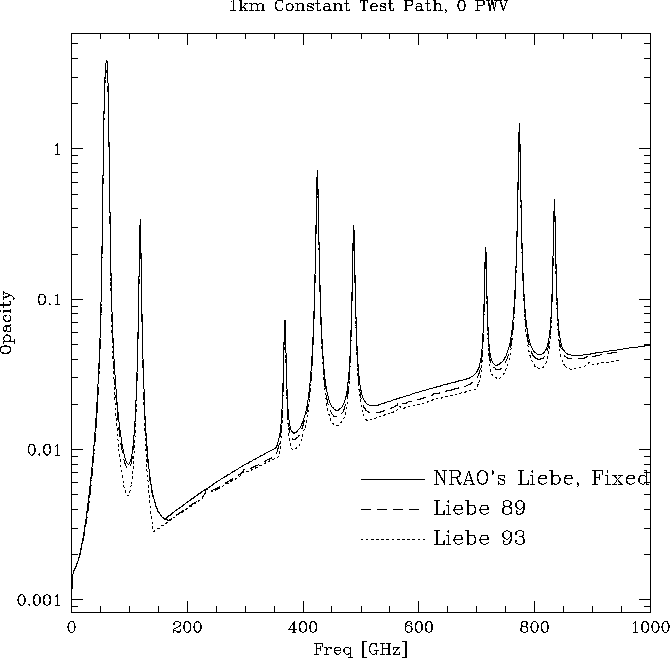
Figure 5: Opacity as a function of frequency for a 1 km horizontal
test path through completely dry air after correcting the
NRAO code.
After correcting these two errors (the nonphysical line shape cutoff and the erroneous conversion between relative humidity and water vapor density), NRAO's version of the Liebe code actually agreed fairly well with ATM's Liebe 89 model (see Figure 6).
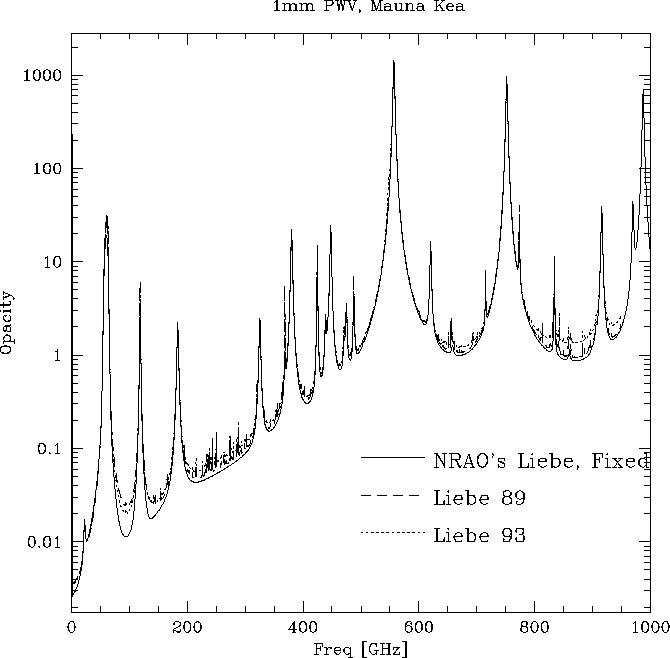
Figure 6: Opacity as a function of frequency with 1 mm PWV above Mauna Kea,
for NRAO's Liebe model after the two errors were corrected,
and the two Liebe models in ATM.
Richard Hills has made simultaneous measurements of the opacity at 225 GHz and at 692 GHz in Millimeter Valley near the Mauna Kea summit. The 225 GHz observations were made with the NRAO/MMA site testing radiometer at the CSO site, and the 692 GHz measurements were made with the JCMT. The data were taken before the CSO took over maintenance of the 225 GHz radiometer. The data have been posted in various public places and given to different people. We got our digital copy of the data from Bob Brown. These data are reproduced in Figure 7.
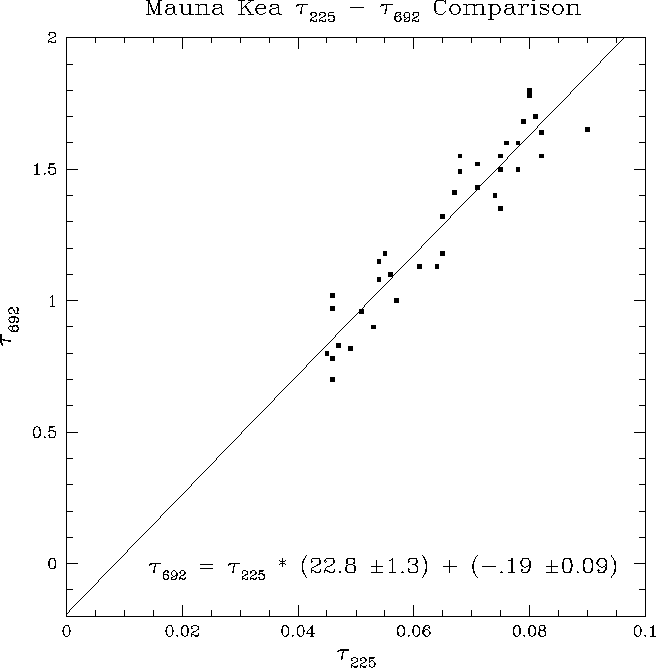
Figure 7: Comparison of the opacity at 225 GHz and at 692 GHz
near the Mauna Kea summit.
We expect a linear relationship between the two opacities, but
not a simple scaling since there are wet and dry opacity terms
at both frequencies.
The best fit line for these data are
![]()
We would like very much to finish our story in a nice and tidy fashion by saying that the empirical relationship derived from Hills' data agrees with one of our fixed up models, but it doesn't. Hills' relationship actually agrees perfectly with the old (ie, buggy) NRAO version of the Liebe model.
Assuming that the form of the water vapor distribution above the site
does not change, the transmission models produce, for each frequency
requested, dry opacity terms due to atmospheric constituents which do
not change with time, and wet opacity terms, which scale with the
amount of precipitable water vapor (PWV) in the atmosphere, which is
highly variable:
![]()
For Mauna Kea, the NRAO's buggy version of the Liebe model yields:
![]()
![]()
which results in the relationship:
![]()
which compares very favorably with Hill's empirical result.
ATM's Liebe 89 predicts that
![]()
and ATM's Liebe 93 predicts that
![]()
both in significant disagreement with Hill's empirical result.
To summarize our predicament:
| Measured | 650 GHz | 850 GHz | |||||
| Quartile | 225 GHz | Old NRAO | ATM | ATM | Old NRAO | ATM | ATM |
| | Liebe 89 | Liebe 89 | Liebe 93 | Liebe 89 | Liebe 89 | Liebe 93 | |
| .10 | 0.028 | 0.25 | 0.49 | 0.44 | 0.29 | 0.47 | 0.51 |
| .25 | 0.036 | 0.35 | 0.72 | 0.65 | 0.38 | 0.66 | 0.73 |
| .50 | 0.054 | 0.56 | 1.24 | 1.21 | 0.59 | 1.10 | 1.22 |
| South Pole | Mauna Kea | Chajnantor | ||||
| Quartile | 1992 | 1992 | Average | Average | 1995 | 1995 Oct |
|
| Apr-Sep | Other | Jan-Jun | Jul-Dec | Apr-Sep | - 1996 Mar |
| .25 | 0.040 | 0.052 | 0.052 | 0.079 | 0.032 | 0.046 |
| .50 | 0.046 | 0.062 | 0.076 | 0.129 | 0.044 | 0.077 |
| .75 | 0.055 | 0.076 | 0.136 | 0.245 | 0.066 | 0.138 |
References
Cernicharo, J., 1988, Thèse de Docortat d'État. Université Pierre
et Marie Curie.
Chamberlin, R. et al, 1997, ``The 492 GHz
Atmospheric Opacity at the Geographic
South Pole'', Astrophysical Journal, 476, 428-433.
Liebe, H.J., 1989, ``MPM-An atmospheric millimeter-wave propagation
model'', Int. J. Infrared and Millimeter Waves, 10,
631-650.
Liebe, H.J.et al, 1993, AGARD
52![]() meeting, Palma de Mallorca, Spain.
meeting, Palma de Mallorca, Spain.
Pardo, J.R., 1996, Thèse de Docortat. Université Pierre
et Marie Curie.
Serabyn, G. et al, 1997, ``Submillimeter FTS Measurements
of Atmospheric Opacity above Mauna Kea'', Applied Optics, submitted.
Shwab, F., and Hogg, D., 1988, MMA Memo 51, ``Millimeter-Wave
Seeing Inferred from Radiosonde Observation-Preliminary Results''.
Shwab, F., and Hogg, D., 1989, MMA Memo 58, ``Millimeter
Wave Atmospheric opacity and Transparency Curves''.