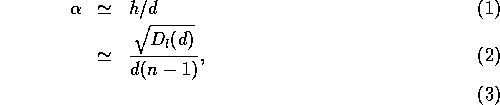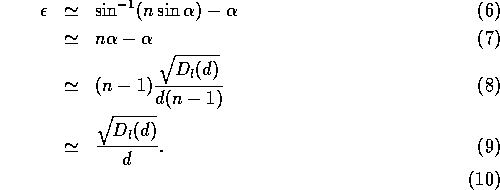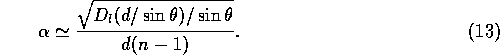Back to Memolist

MMA Memo 186: Calculation of Anomalous Refraction on Chajnantor

M.A. Holdaway
National Radio Astronomy Observatory
949 N. Cherry Ave.
Tucson, AZ 85721-0655
email: mholdawa@nrao.edu

September 30, 1997

Abstract:

We have investigated the effects of inhomogeneously distributed water vapor, as characterized by our 11.2 GHz site testing interferometer database, upon antenna pointing. This effect, known as ``anomalous refraction'', has been seen at poorer sites with millimeter wavelength telescopes for years (Altenhoff et al. 1987). Because of the structure of atmospheric turbulence, the pointing error in arcseconds will be smaller for larger antennas, but the pointing error will be larger in terms of the fraction of the beam size. The time scale of the pointing error will be nearly the time required for the atmosphere to cross the dish. To first order, water vapor is non-dispersive, so the anomalous refraction pointing errors will be independent of frequency. However, there is mild dispersion in the submillimeter, resulting in slightly larger pointing errors in the submillimeter windows. For an 8 m dish on the Chajnantor site, the atmospheric contribution to the pointing errors will usually be well under an arcsecond, except during poor weather and while observing at the lowest elevation angles.

Introduction

Recently, there has been some concern over the stringent 1 arcsec pointing error requirement on the MMA antennas. While the pointing requirement is one of the main drivers for the antennas, it is clear that we need the good pointing to make high quality mosaic images at millimeter and submillimeter wavelengths. Some investigators have questioned if 1 arcsec pointing can even be useful at all, given that the turbulent atmosphere causes both the synthesized beam and the primary beam to dance about the sky. If the columns of water vapor above two antennas are different, a phase error will result, effectively causing that baseline's contribution to the synthesized beam to shift on the sky. If there is a gradient in the water vapor distribution above one antenna, anomalous refraction, or a shift in the apparent pointing, will result (see Figure 1). Since both effects are caused by inhomogeneously distributed water vapor, we can predict the magnitude of these effects from the site testing interferometer data (Holdaway et al., 1995). Simulations of mosaicing with phase errors appropriate to the Chajnantor site have been found to have little effect on imaging, which is dominated by the physical pointing errors of the antennas (Holdaway, 1997). Here, we investigate the severity of the pointing errors caused by anomalous refraction.

Anomalous refraction (Altenhoff et al., 1987) has been seen with several millimeter wavelength telescopes. If a wedge of water vapor falls across the antenna's line of site, refraction occurs. There is nothing special about these wedges, they are just part of the distribution of turbulent water vapor, and as such go back and forth very quickly, as opposed to a systematic, persistent wedge. Hence, anomalous refraction causes pointing errors with time scale approximately equal to the time it takes the atmosphere to cross the antenna. Indeed, some of the early investigations of anomalous refraction found that the pointing error reversed itself before the dish could scan over a bright quasar, producing an apparent double beam.

We approximate the instantaneous phase screen as a wedge. Figure 2 shows an example of an actual phase time series which, assuming frozen turbulence, has been converted into a one dimensional slice through a spatial phase screen. The phase bump directly over the antenna is assumed to be a wedge, and smaller scale deviations from the wedge will participate in Ruze scattering, making the beam wider.

Zenith Case

In Figure 3 we work through the mathematics of the model for zenith observations. The geometry of our wedge of water vapor is set by the angle 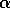, which can be related to the dish diameter d and the path length structure function 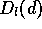through:
 
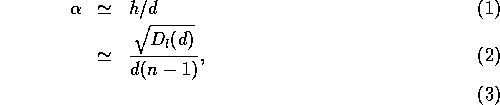
where n is the index of refraction. Snell's law relates the angl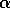e between the incident ray and the line perpendicular to the wedge to the angle 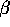between the refracted ray and the normal:

The pointing error due to anomalous refraction is given by

Then, using small angle approximations,
 
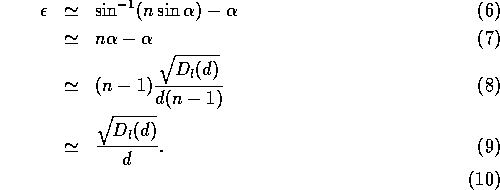
The path length structure function is typically approximated as a power law in the baseline (here d), but the amplitude and power law exponent change with the atmospheric conditions:

On the Chajnantor site, the median structure function power law exponent is 1.2 (or the rms path length, 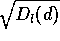, varies as 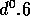. Hence, as the dish size increases, the amount of anomalous refraction actually decreases as 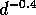. However, the anomalous refraction does not decrease as fast as the beam size, so the pointing error as a fraction of the beam will increase as .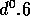

Non-Zenith Case

Now, the zenith case is the best case with the least amount of anomalous refraction. We also consider worse cases, with arbitrary observing elevation and the wedge in the plane of the line of sight (see Figure 4). We spare the reader the mathematical details, but point out a few of the complicating factors:

• the effective baseline at which the path length structure function must be evaluated is 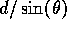, where 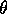is the observing elevation angle.
• the structure function depends upon elevation as 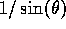(ie, Holdaway and Ishiguro, 1995).
• small angle approximations cannot be used, except for .

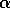A person adept in trigo-algebraic manipulations might have gotten the expression in a nicer form, but the computer doesn't mind that the expression for the anomalous refraction pointing error for non-zenith observations is given by
 
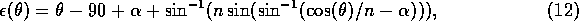
with 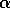now related to the structure function via

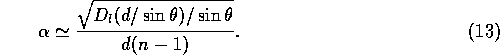
Equation 12 reproduces the results of Equation 9 at the zenith.

From our site testing efforts on Chajnantor, we have a good statistical knowledge of the path length structure function. Even though we measure the interferometric phase on a 300 m baseline, we sample the phase with 1 s integrations. The temporal fluctuations on 1 s timescales are interpreted to be spatial structure flowing over the interferometer. The signal to noise on 1 s is not always sufficient to characterize the spatial fluctuations on size scales of 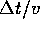, but when there is high enough SNR, we find that the temporal structure function is always well fit by a power law. Hence, low SNR conditions still permit a fit to the higher SNR medium to long time scale fluctuations and extrapolation back to the short time scales we are interested in here. A comparison between the temporal structure function and the single point we measure on the spatial structure function at 300 m effectively permits us to solve for the velocity, or to convert the temporal structure function into the spatial structure function, which is the required quantity for this analysis.

We have calculated the rms pointing error due to anomalous refraction on the Chajnantor site for the three quartiles of the rms path length fluctuations, for a range of elevation angles, and for dish diameters 8 m, 12 m, 15 m, and 50 m. The three smaller dish diameters are under discussion for building on the Chajnantor site, and the 50 m calculations are for the benefit of the LMT project. In Table 1 we present the results for the pointing error in arcseconds, along with the fraction of the pointing specification in parentheses. The pointing specification is taken to be 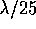at 300 GHz for the three smaller dishes (1 arcs, 0.67 arcs, and 0.53 arcs respectively) and 0.6 arcs over 2 hours for the 50 m dish. If the LMT's site has worse phase stability than the Chajnantor site, then the pointing errors due to anomalous refraction will be larger than the values quoted here.

Also presented in Table 1 are the quartile rms atmospheric path length differences across the dish, in microns. These numbers can get quite large, 50-100 microns for the 50 m dish. As stated earlier, the wedge shape (ie, tilt) will dominate, but there is also structure on the smaller scales deviating from the wedge. These smaller scale deviations will behave as surface errors, effectively broadening the primary beam. Since physical surface errors on the antenna affect the path length twice (pre and post main reflector) and these atmospheric fluctuations only affect the path length once (except for the presumably rare case where the turbulent water vapor is dominated by thin layer between the main reflector and the subreflector!) the residual path length deviations must be divided by two before applying the Ruze formula. We have not investigated this effect further, as we expect it to usually be small for the small interferometric dishes.

 

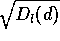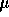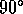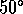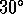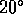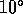25% 8.8 0.22 0.31 0.52 0.81 1.73

(0.22) (0.31) (0.52) (0.81) (1.73)

50% 18.0 0.47 0.64 1.07 1.65 3.55

(0.47) (0.64) (1.07) (1.65) (3.55)

75% 39.2 1.01 1.40 2.31 3.59 7.75

(1.01) (1.40) (2.31) (3.59) (7.75) d = 12m, (pointing spec = 0.67 arcs) elevation Q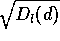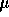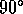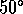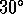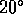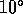

25% 11.2 0.20 0.26 0.44 0.68 1.47

(0.29) (0.39) (0.66) (1.00) (2.20)

50% 22.9 0.39 0.55 0.90 1.40 3.02

(0.58) (0.81) (1.40) (2.11) (4.50)

75% 50.0 0.86 1.20 1.98 3.05 6.59

(1.30) (1.79) (3.00) (4.60) (9.91) d = 15m, (pointing spec = 0.53 arcs) elevation Q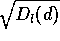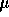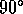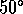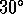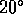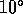

25% 12.8 0.17 0.25 0.40 0.62 1.34

(0.31) (0.47) (0.75) (1.17) (2.51)

50% 26.2 0.36 0.49 0.82 1.27 2.76

(0.68) (0.92) (1.53) (2.39) (5.16)

75% 57.2 0.78 1.09 1.81 2.79 6.02

(1.46) (2.05) (3.39) (5.24) (11.3) d = 50m, (pointing spec = 0.6 arcs) elevation Q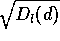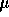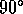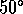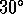

25% 26.3 0.10 0.16 0.25 0.39 0.83

(0.17) (0.26) (0.41) (0.65) (1.20)

50% 53.9 0.22 0.31 0.51 0.79 1.70

(0.37) (0.52) (0.85) (1.32) (2.84)

75% 118. 0.48 0.68 1.12 1.73 3.72

(0.80) (1.12) (1.86) (2.88) (6.20)

 

Dispersion

We have assumed that the water vapor is non-dispersive, or that the anomalous refraction is independent of frequency. This is nearly true up to 300 Ghz, but begins to break down above 300 GHz, and the pointing errors due to anomalous refraction will be about 30% larger in the submillimeter windows due to large values of the index of refraction of water vapor.

Time Scales

To first order, the time scale of the anomalous refraction pointing errors will be the time it takes the atmosphere to cross the dish, which is on the order of a second. The details of the structure of the atmosphere will increase the pointing error time scale, especially for small dishes. We can calculate the time scale of the pointing errors using the raw phase monitor data. The pointing errors are proportional to the spatial derivative of the phase screen evaluated on spatial scales of the dish diameter. The pointing error time scale can be estimated from these time series (see Figure 5 and Table 2. These pointing errors will be more or less random over the array. For observations which are long compared to the pointing error time scale, the pointing errors will have a minimal effect, as they are both random in time and with antenna. For observations which are short compared to the pointing error time scale, as for On-The-Fly mosaicing or total power work, the pointing errors will be more problematic. Finally, for a large single dish performing On-The-Fly imaging, the pointing errors are most damaging, as they persist over several beams on the sky, but not long enough to be calibrated, and there are no other antennas to average down spatially random pointing errors with.

 

Antenna Diameter Average Pointing

[m] Time Scale [s]

10 2.7

20 3.9

30 5.0

50 6.7

 

Correcting for Anomalous Refraction Pointing Errors

For arrays of small antennas on a good site, there is little point to correcting the anomalous refraction. However, for a single large antenna, pointing errors caused by anomalous refraction may limit the performance of the antenna some of the time. If one could measure the distribution of water vapor above the antenna on second time scales, one could correct for the pointing in real time or in data post-processing One could do this by mounting four or five 22 GHz or 183 GHz (depending upon the quality of the site) water vapor spectrometers of the sort David Woody is making, at the edge of the large single dish, and possibly one on the back of the subreflector.

References

Altenhoff, W.J., et al., 1987, ``Observations of anomalous refraction at radio wavelengths'', A&A 184, 381.

Holdaway, M.A., and Ishiguro, M., 1995, MMA Memo 127, ``Experimental Determination of the Dependence of Tropospheric Path Length Variation on Airmass''.

Holdaway, M.A. et al., 1995, MMA Memo 129, ``Data Processing for Site Test Interferometers''.

Holdaway, M.A. et al., 1997, MMA Memo 178, ``Effects of Pointing Errors on Mosaic Images with 8m, 12m, and 15m Dishes''.

  

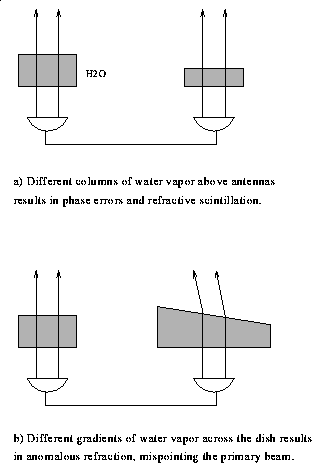
Figure 1: Water vapor distributions resulting in phase errors and anomalous refraction.

  

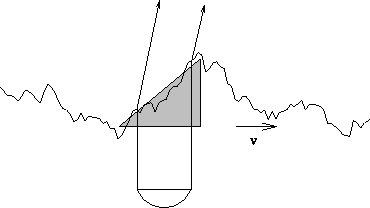
Figure 2: An example water vapor column screen derived from phase monitor time series data, showing the wedge approximation.

  

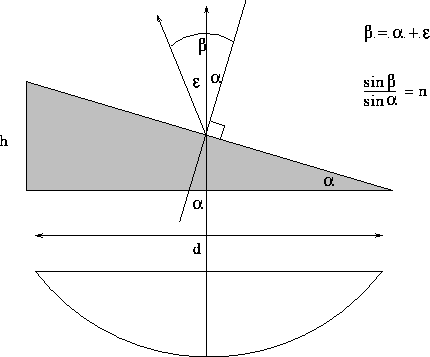
Figure 3: Geometry for the anomalous refraction calculation for the zenith.

  

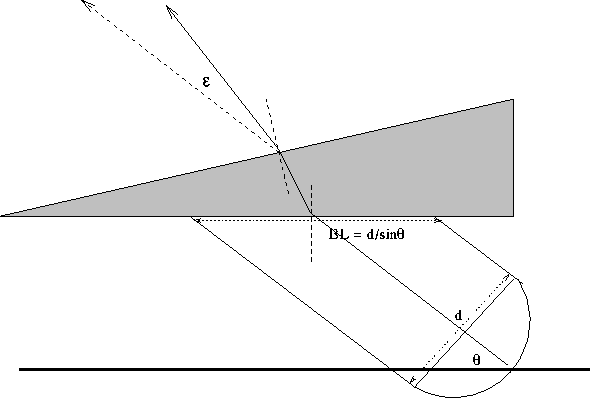
Figure 4: Geometry for the anomalous refraction calculation away from the zenith.

  

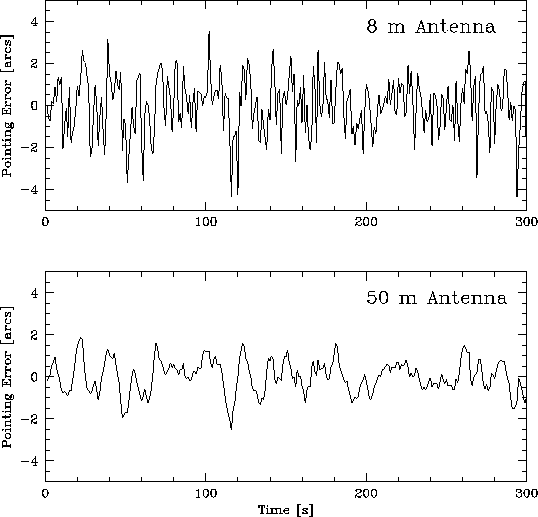
Figure 5: A time series of pointing errors as calculated for an 8 m and a 50 m dish from site testing data during poor conditions. The larger dish has smaller pointing errors in arcseconds (larger as a fraction of the beam), but the time scale of the fluctuations are larger, and therefore more damaging to mapping work.