M.A. Holdaway
National Radio Astronomy Observatory
949 N. Cherry Ave.
Tucson, AZ 85721-0655
email: mholdawa@nrao.edu
April 21, 1997
We investigate the distribution of atmospheric coherence times for long baselines and the fraction of time a given baseline will be phase stable during the months of best phase stability. The coherence times set a lower limit to the time over which the MMA electronics must allow stable integration. It is probable that radiometric phase compensation will further increase the requirements on the MMA electronics. The best quartile coherence time (at 90% sensitivity) at 100 GHz is about 4 minutes, while best quartile coherence time at 650 GHz is only 8 s.
Phase errors on long time scales can be calibrated out, but phase
errors on short time scales result in loss of coherence or
decorrelation (Lay, 1997). Baseline based phase fluctuations of rms
radians will result in decorrelation of magnitude
(Thompson, Moran and Swenson, 1986). The
main effects of the decorrelation are loss of sensitivity and errors
in imaging. The effects of decorrelation on imaging can largely be
corrected if the rms phase errors are not too much larger than a
radian (Holdaway and Owen, 1995), but lost sensitivity cannot be
recovered. For this reason, several groups have invested great effort
to remove the phase errors radiometrically prior to correlation.
The two main sources of decorrelating phase errors are the atmospheric phase fluctuations and the electronics, notably the LO. We should design the LO and electronics such that it is significantly more phase stable than the atmosphere during good conditions. This memo converts the phase monitor data taken with the 300 m site testing interferometer into estimates of the distribution of the coherence time at 100, 230, 345, and 650 GHz. If the coherence time is longer than the baseline crossing time, that baseline will be phase stable for long periods of time. We also present the fraction of time which certain baseline lengths are phase stable.
For every 600 s block of site testing interferometer data, we
calculate the temporal phase structure function and fit a power law to
the short time scale part (Holdaway, Radford, Owen, and Foster, 1995).
On time scales long compared to the crossing time of the
interferometer, the rms phase essentially saturates. The spatial (and
temporal) structure functions should flatten for baselines (or time
scales) longer than the size scale of the turbulent layer, but we see
no evidence for such a flattening out to 300 m. Hence, we assume that
our simple one part power law describes the phase errors, and we also
extrapolate beyond the 
30 s crossing time when necessary. If
the phase structure function does flatten out, this will not change
any of the coherence times which are less than 30 s, but will
increase some of the coherence times which are longer than 30 s.
The root temporal structure function of the interferometer phase
is fit by
where 
is the interferometer phase at some time t, and a
and 
are the amplitude and power law exponent of the temporal phase
structure function. The factor of 
enters because we are differencing
two interferometer phases measured at two different times. Then the root
temporal phase structure function (ie, the rms phase which one would expect
on a long baseline on some time scale t) is
For long baselines, the time scale over which the rms phase errors
exceed some value 
, or the coherence time, is given by
In this case, a ``long baseline'' is one for which the atmospheric
crossing time is long compared to the coherence time. For each
observing frequency considered, we scale the phase structure function
with frequency non-dispersively. However, Hill and Clifford's (1981)
calculations indicate that the water vapor is moderately dispersive in
the submillimeter. For example, at 345 GHz, the wet delay is expected
to be about 8% larger than the wet delay at 10 or 100 GHz. At
490 GHz, the delay will be about 20% larger than at 100 GHz. While
this dispersion is a moderate effect in our coherence time estimates,
the dispersion could be a major effect when extrapolating the phase
from low frequencies to high frequencies.
What value should we use for ? Since different
applications may have different coherence requirements, we look at a
range of : 11.5
results in 0.98 sensitivity,
26.3 results in 0.90 sensitivity, and 67.5 results in 0.50
sensitivity. In this study, we do not address the phase contributions
from the motion of the antenna structure or the electronics, but look
only at the atmosphere. Coherence time will also be a strong function
of frequency, so we calculate coherence times at 100, 230, 345, and
650 GHz. The cumulative distributions of coherence times for these
different circumstances are shown in Figures 1-2 for the winter months
(May, June, and July, the months of best phase stability) at
Chajnantor. The median and 75% coherence times for 90% sensitivity
are shown in Table 1. The 75% coherence time (the
coherence time is this long or longer for the 25% best conditions)
will be approximately equal to the night time median coherence time as
the daytime conditions are almost always worse than the night time
conditions. For the millimeter frequencies, the coherence times are
reasonably large, typically about a minute or longer. However, in the
submillimeter, the coherence times become very short, even at the 75%
level (25 s at 345 GHz and 8 s at 650 GHz). This indicates that
submillimeter observations will be done only during the really good
conditions (ie, the winter nights), and even then, fast switching
with 10 s cycle times will be pushed very hard.
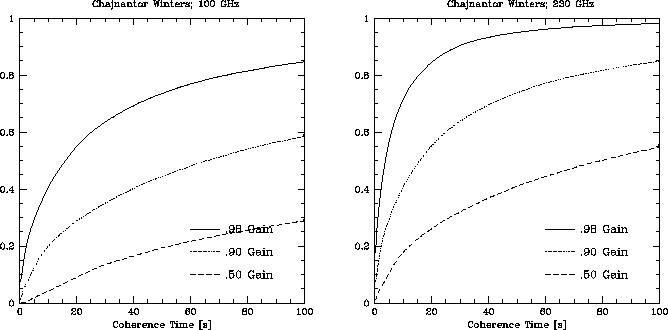
Figure 1: Cumulative distribution function of atmospheric coherence
time for 98%, 90%, and 50% gain for Chajnantor during the winter
season at 100 GHz and 230 GHz.
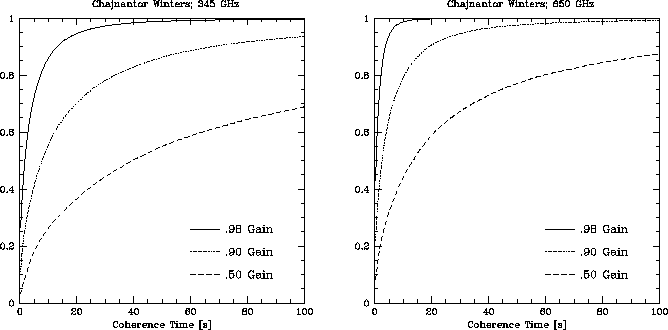
Figure 2: Cumulative distribution function of atmospheric coherence
time for 98%, 90%, and 50% gain for Chajnantor during the winter
season at 345 GHz and 650 GHz.
 [GHz] | 50%  [s] | 75% [s] |
| 100 | 66 | 228 |
| 230 | 16 | 53 |
| 345 | 8 | 25 |
| 650 | 2.5 | 8 |
The above analysis is for baselines with atmospheric crossing times
which are longer than the coherence time, and does not apply to shorter
baselines. The root spatial phase structure function is defined as
where 
is the distance between antennas and the exponent is the same
for the spatial and temporal structure functions.
A short baseline will be said to be ``phase stable'' when
In this case, arbitrarily long integrations can be made (practically,
this is tens of minutes). Table 2 shows the fraction of time selected
baselines and frequencies will be phase stable during the winter
months.
|
[GHz] | BL [m] | 98% Gain | 90% Gain | 50% Gain |
| 100 | 25 | 0.88 | 0.97 | 1.00 |
| 100 | 50 | 0.80 | 0.94 | 1.00 |
| 100 | 100 | 0.69 | 0.89 | 0.99 |
| 100 | 200 | 0.54 | 0.80 | 0.96 |
| 100 | 400 | 0.37 | 0.69 | 0.91 |
| 100 | 800 | 0.22 | 0.54 | 0.83 |
| 100 | 1600 | 0.12 | 0.39 | 0.72 |
| 230 | 25 | 0.69 | 0.88 | 0.97 |
| 230 | 50 | 0.54 | 0.80 | 0.95 |
| 230 | 100 | 0.36 | 0.69 | 0.90 |
| 230 | 200 | 0.19 | 0.54 | 0.83 |
| 230 | 400 | 0.08 | 0.37 | 0.72 |
| 230 | 800 | 0.03 | 0.22 | 0.58 |
| 230 | 1600 | 0.01 | 0.12 | 0.43 |
|
[GHz] | BL [m] | 98% Gain | 90% Gain | 50% Gain |
| 345 | 25 | 0.54 | 0.80 | 0.94 |
| 345 | 50 | 0.36 | 0.69 | 0.90 |
| 345 | 100 | 0.18 | 0.54 | 0.83 |
| 345 | 200 | 0.07 | 0.37 | 0.73 |
| 345 | 400 | 0.02 | 0.21 | 0.59 |
| 345 | 800 | 0.00 | 0.10 | 0.43 |
| 345 | 1600 | 0.00 | 0.04 | 0.28 |
| 650 | 25 | 0.25 | 0.62 | 0.86 |
| 650 | 50 | 0.09 | 0.44 | 0.78 |
| 650 | 100 | 0.02 | 0.26 | 0.66 |
| 650 | 200 | 0.00 | 0.12 | 0.50 |
| 650 | 400 | 0.00 | 0.04 | 0.33 |
| 650 | 800 | 0.00 | 0.01 | 0.19 |
| 650 | 1600 | 0.00 | 0.00 | 0.09 |
|
[GHz] | BL [m] | 98% Gain | 90% Gain | 50% Gain |
| 850 | 25 | 0.12 | 0.51 | 0.81 |
| 850 | 50 | 0.03 | 0.32 | 0.71 |
| 850 | 100 | 0.00 | 0.15 | 0.56 |
| 850 | 200 | 0.00 | 0.05 | 0.38 |
| 850 | 400 | 0.00 | 0.01 | 0.22 |
| 850 | 800 | 0.00 | 0.00 | 0.11 |
| 850 | 1600 | 0.00 | 0.00 | 0.05 |
The investigation of radiometric phase compensation is still ongoing, so it is not yet possible to quantify the improvements to the coherence time. However, it is expected that radiometric compensation will permit significantly increased integrations.
References
Holdaway, M.A., and Owen, F.N., 1995, ``Correcting for Decorrelation
Due to Atmospheric Phase Errors, MMA Memo 136.
Holdaway, M.A., Radford, Simon J.E., Owen, F.N., and Foster, Scott M.,
1995, ``Data Processing for the Site Test Interferometers'', MMA Memo
127.
Lay, O.P., 1997, ``Phase Calibration and Water Vapor Radiometry for
Millimeter-Wave Arrays'', accepted to A&A.
Thompson, Moran, and Swenson, 1986, Interferometry and Synthesis in
Radio Astronomy, John Wiley & Sons, New York.