M.A. Holdaway
National Radio Astronomy Observatory
949 N. Cherry Ave.
Tucson, AZ 85721-0655
email: mholdawa@nrao.edu
Masato Ishiguro, Naomasa Nakai, and Satoki Matsushita
Nobeyama Radio Observatory
National Astronomical Observatory
Minamimaki, Minamisaku
Nagano 384-13, Japan
email: (ishiguro, nakai, satoki)@nro.nao.ac.jp
August 1, 1996
We use the surface water vapor pressure measured by weather stations at 4060 m and 4200 m elevation at Rio Frio to estimate the water vapor scale height. We also estimate the water vapor column above the array and attempt to correlate it with the water vapor column inferred from the 220 GHz opacity.
The surface water vapor pressure is inverted some 20% of the time at night and some 35% of the time during the day, making scale height measurements impossible. Of the non-inverted conditions, the night time water vapor scale height is typically 1 km, and the day time water vapor scale height is about 2 km. The scale height during summer days is about 2.5 times larger than during winter days, while the night time scale height shows no seasonal variation. The integrated solar flux, averaged over the summer half of the data, is about 1.8 times higher than during the winter, indicating that the input of solar energy is related to the diurnal and seasonal variations of the water vapor scale height. The water vapor column estimated from the water vapor pressure measurements show a very rough agreement with the opacity measurements. The nature of the correlation is different between day and night time conditions.
Some very complicated events are seen in which either the opacity or the surface water vapor pressure changes dramatically while the other remains constant. Strategically placing more weather stations at higher elevations on nearby mountains would provide crucial information on inversion layers which would help in the interpretation of the water vapor and opacity data and would provide important insights into the atmosphere. Any new weather stations should add atmospheric pressure to the meteorological parameters already sampled by the existing stations.
Before the first millimeter wavelength site testing radiometers were built to gauge the millimeter opacity at a potential telescope site (ie, Kono et al., 1995), it was common to estimate the millimeter wavelength opacity from a water vapor column height derived from integration of the water vapor pressure with height as measured by radiosonde. This method has the problem of relying upon atmospheric transmission models to convert from the water vapor column to the actual opacity, but it provided reasonable estimates of the opacity, especially if the radiosonde were launched at a site and elevation near the site of interest.
The Rio Frio site in northern Chile, one of several sites to which the world millimeter astronomical community is now turning its attention, is equipped with a radiometer and radio seeing monitor at 4120 m, a weather station 2.1 km to the west at 4200 m (referred to in this memo as weather station 1), and a weather station 2.5 km to the east at 4060 m (referred to here as weather station 2; see Figure 1). The weather stations measure temperature, wind speed and direction, solar flux, and water vapor pressure, which are recorded in 20 minute intervals (Nakai et al., 1995). Atmospheric pressure is not recorded. With this arrangement of test equipment, it is possible to estimate the water vapor scale height, to integrate the water vapor above the test equipment, and to correlate the water vapor with the opacity. Such an experimental setup is much cheaper and provides much more data than radiosondes could, but is highly dependent upon some assumed form for the water vapor distribution with height. This memo reports on preliminary efforts to correlate the water vapor measurements with the opacity, hinting at the complications which arise, and pointing to the possibility of deploying more weather stations to cover a greater range of elevations to more adequately sample the atmosphere.
In order to compare meteorological data from the two weather stations and the opacity from the radiometer, we interpolated data from the lower weather station and the radiometer onto the sampled times of the upper weather station. Interpolation was required as the water vapor pressure could change substantially over the time between measurements at the two stations.
Typical values of the surface water vapor pressure at Rio Frio range between 0.2 and 5 hecto Pascals. We estimate the noise in the water vapor pressure measurements to be less than 0.02. Little is known about the long term stability of the instrument, but if long term instabilities existed, we would see many more inverted water vapor pressure conditions than we actually do (see below). Typical values of the opacity at Rio Frio range from 0.02 to 0.1. We estimate the errors on the low opacity measurements made with the NRAO radiometer to be less than 0.001 (Foster, 1996), and the NRO radiometer at Rio Frio probably has similar error levels.
The weather station data we analyzed runs from 1995 July 2 to 1995 December 19. Due to the problems of operating complicated scientific test equipment remotely, the radiometer was either not operating or only taking data over part of each day for most of the time. Hence, there are only a few periods when the opacity time series can be compared with the water vapor measurements for several days continuously. Figures 2 through 4 show the longest stretches of continuous data from the weather stations and the radiometer.
These data show some very rich trends. Figure 2 shows little correspondence between the surface water vapor pressure and the opacity. The surface water vapor increases dramatically at day 185.2 (5am) at both weather stations, but there is little change in the opacity. There is a similar surface water vapor increase at day 185.7 (5pm). The opacity changes very little with this increase in surface water vapor, but as the surface water vapor decreases again, the opacity shows a correlated decline. The surface water vapor rise at 185.2 can be attributed to some purely surface phenomenon, such as dew or fog. The surface increase at 185.7 can be interpreted as a moist inversion layer which was initially above the upper weather station but is now descending upon the weather stations. Note that it hits the upper weather station first. Shortly after the surface water vapor hits a flat maximum, the opacity starts to drop, consistent with a layer of roughly constant water vapor slowly moving down the site's slope to the east. Finally, the end of this layer is seen as the surface water vapor also drops back down.
In Figure 3, we can see several instances of the afternoon rise in opacity and surface water vapor pressure atop a gradual increase in opacity throughout the3.5 day period. During two of the afternoon peaks, the opacity shows a double peaked structure and the surface water vapor is inverted during the second peak. The water vapor pressure time series usually shows much more dynamic range than the opacity.
There are broad features in Figure 4 which show very good correlation between water vapor pressure and opacity, while other features show almost no correlation.
If we assume the water vapor is distributed exponentially with height, we can estimate the water vapor scale height from the ratio of the water vapor pressure measured at the two weather stations. However, some of the time the upper WS1 has higher water vapor pressure than the lower WS2, which does not permit any scale height calculation and is due to a vertical inversion, local surface effects, or horizontal variation. Figure 5 illustrates that such inverted conditions occur most often during the day. Figure 6 shows the first, second, and third quartiles of the calculated scale height as a function of hour of the day. About 500 measurements over 180 days have gone into each hour. The scale height is typically 1 km all through the night, but increases to about 2 km during the day. The night time scale height is roughly the same for and summer and winter, but the day time scale height is about 2.5 times as high in the summer as in the winter (see Figure 7). The integrated solar flux over the summer and winter periods differed by a factor of about 1.8 (see Figure 8), which implies that the change in the solar radiation has a lot to do with the diurnal and seasonal dependence of the water vapor scale height.
The precipitable water vapor can be calculated by assuming an exponential distribution, solving for the scale height based on the difference in water vapor pressure at the two weather stations, and integrating the water vapor pressure profile through the atmosphere. The scaling from water vapor pressure to PWV in millimeters is approximately
![]()
where T is the atmospheric temperature, h is a distance element along the line of site,, in meters, and WVP is the measured water vapor pressure in hecto Pascals. Furthermore, assuming that the opacity at 220 GHz is related to the precipitable water vapor in millimeters as
![]()
it is possible to look for a correlation between the two methods of calculating the PWV. We don't really expect the two methods to agree that well since an exponential atmosphere is usually a vast oversimplification. However, when the two values of PWV do agree, that implies the atmosphere has a smooth profile of PWV with height, and when they don't agree something more complicated, like an inversion layer or surface effects, may be present.
Figure 9 shows the daytime correlation between the PWV obtained by integrating an exponential distribution of water vapor pressure and the PWV obtained from the opacity, and Figure 10 shows the night time correlation. This represents the subset of data for which the calculated water vapor scale height was between 100 m and 5000 m. All inverted water vapor conditions were rejected from this analysis. During the day time, we actually see some correlation, though the water vapor pressure method overestimates the integrated water vapor. We would expect a similar result if there were excess surface water vapor. (Excess surface water vapor would greatly limit the usefulness of this method.) During the night time, we see some sort of correlation, but the water vapor pressure method underestimates the precipitable water vapor for most of the data points.
It is clear that this sort of analysis can be very fruitful in understanding the details of the atmosphere at a potential millimeter interferometer site. Such a detailed understanding of the atmosphere is important to planning phase calibration strategies for the future millimeter arrays.
Our rough correlation between integrated precipitable water vapor and opacity suggest that the measurements often reflect the meteorological values in the free atmosphere, but either that the water vapor distribution above the site is not a simple exponential or that the measurements are partially influenced by surface effects or horizontal variations. Since both the Rio Frio and the Chajnantor site have high mountains nearby, it is possible to deploy more weather stations at still higher elevations. With four or five weather stations sampling the meteorological data over an elevation range of 1000 m, we should be able to get a good picture of the distribution of the water vapor over the site.
Our data clearly indicate that the water vapor pressure can change dramatically on very short time scales. Small errors in the time or calibration of the weather stations could result in significant errors, espcially in quantities derived from differences or ratios in the measured values, such as the water vapor scale height. If we deploy several weather stations in the future, we should perform side-by-side observations to calibrate the instruments and to estimate the errors in the measurements.
It has been suggested that there is often an inversion layer about 500 m above the Chajnantor site. The atmospheric boundary layer and the inversion layer which caps it should have very clear signatures in several measurable quantities (Azad, 1993):
References
Azad, Ram S., 1993, The Atmospheric Boundary Layer for Engineers,
Kluwer Academic Publishers, Dordrecht, pp. 12-34.
Foster, S.M., 1996, ``Error Analysis of the NRAO Tipping Radiometer
Opacity Measurements'', MMA Memo in preparation.
Kono, K. et al., 1995, ``Preliminary Result of Site Testing in
Northern Chile with a Portable 220 GHz Radiometer'', NRO Technical
Report No. 42.
Nakai, N. et al., 1995, ``Measurement of Meteorological Data in Northern Chile (August - October 1994)''.
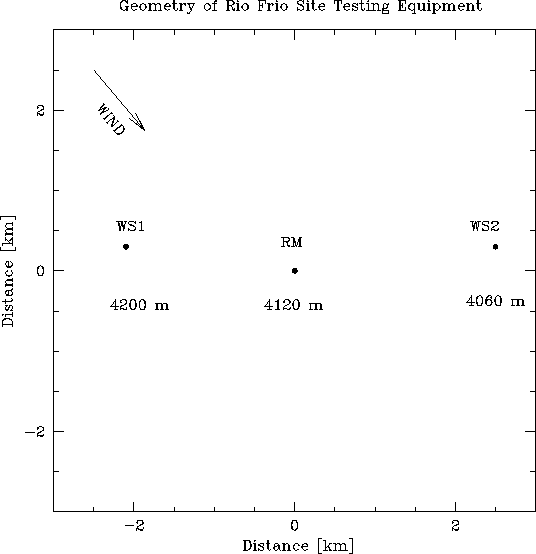
Figure 1: Geometrical layout of the Rio Frio site testing equipment:
WS1 is weather station 1, WS2 is weather station 2, and RM is the
radio seeing monitor and radiometer. Winds are generally from the
northwest. Positions have been taken from Nakai's revised map.
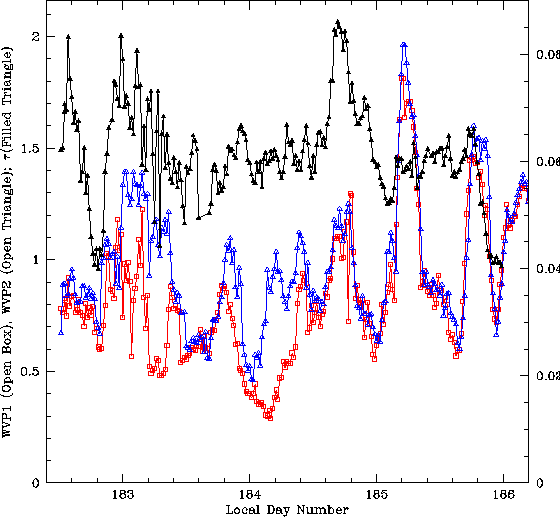
Figure 2: Three and a half days of opacity data (filled triangles) and water vapor
pressures from the upper weather station 1 (open boxes) and the lower weather station 2
(open triangles), (day 183 = July 7, 1995). The left scale is for the water vapor
pressure in hecto Pascals, the right scale is for the opacity.
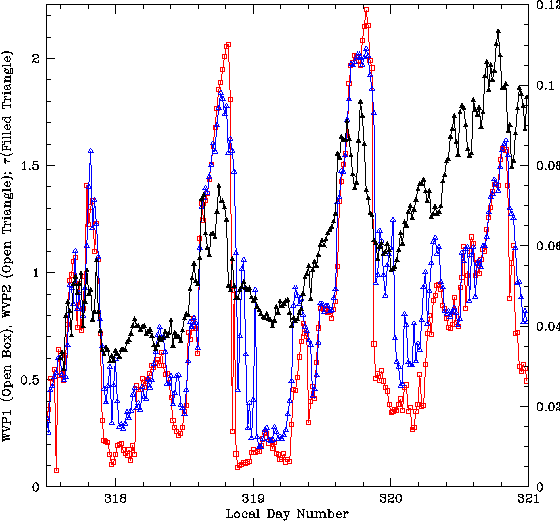
Figure 3: Three and a half days of opacity data (filled triangles) and water vapor
pressures from the upper weather station 1 (open boxes) and the lower weather station 2
(open triangles), (day 318 = November 15, 1995). The left scale is for the water vapor
pressure in hecto Pascals, the right scale is for the opacity.
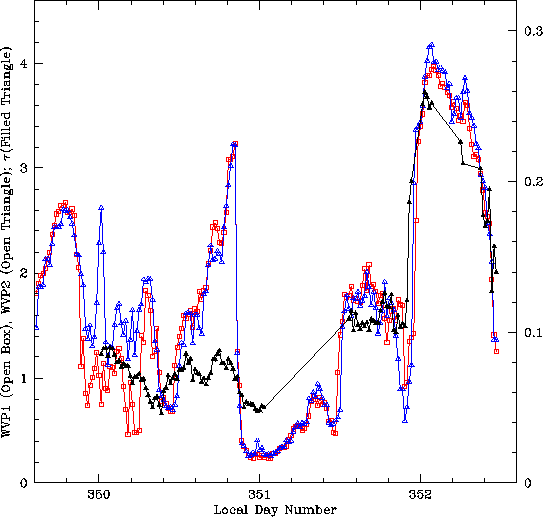
Figure 4: Two and a half days of opacity data (filled triangles) and water vapor
pressures from the upper weather station 1 (open boxes) and the lower weather station 2
(open triangles), (day 350 = December 17, 1995). The left scale is for the water vapor
pressure in hecto Pascals, the right scale is for the opacity.
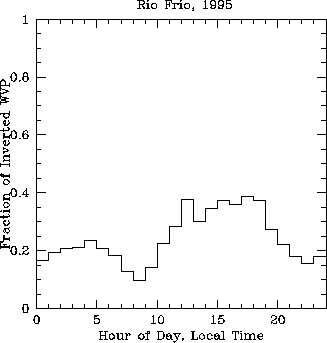
Figure 5: Fraction of time the water vapor pressure is inverted as a function of
local hour.
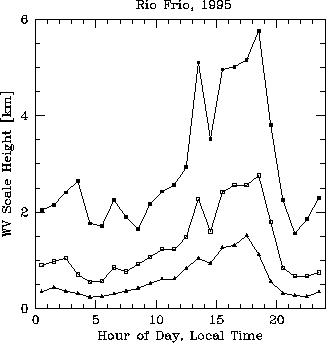
Figure 5: First, second, and third quartiles of the water vapor scale height as a function
of hour.
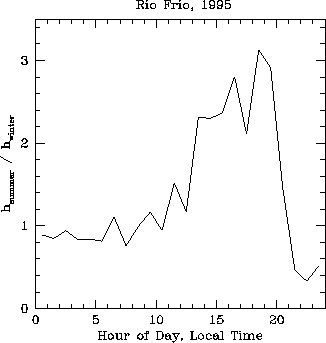
Figure 6: Ratio of the median summer water vapor scale height to the median winter water vapor scale
height vs hour of the day.
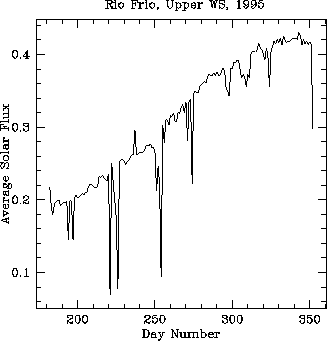
Figure 7: Solar flux in ![]() , averaged over each 24 hour period.
, averaged over each 24 hour period.
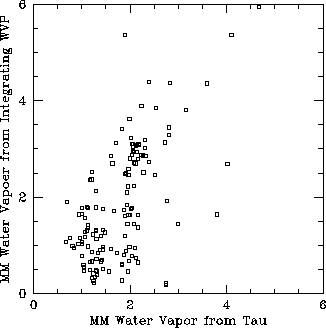
Figure 8: Day time comparison of PWV calculated by integrating the water vapor distribution
vs. PWV calculated from the opacity.
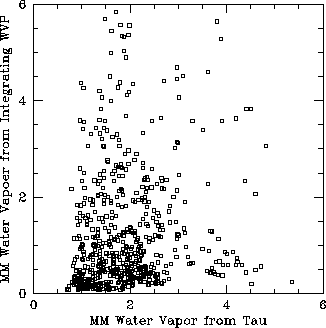
Figure 9: Night time comparison of PWV calculated by integrating the water vapor distribution
vs. PWV calculated from the opacity.