


Next: Acknowledgements
Up: Correcting for Decorrelation Due
Previous: Comparing the Methods
Under the assumption of baseline independent Gaussian residual phase
errors, such as might exist if Welch's total power monitor scheme or
Woody's water vapor spectrometer scheme were employed, a simpler
decorrelation correction might suffice. If the residual phase errors
were antenna dependent or time dependent, then one of the
decorrelation correction methods described here might improve the
imaging.
In the case of fast switching, the residual phase errors are
equal to the square root of the phase structure function
 for short baselines
for short baselines 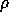 and saturate at
a value of
and saturate at
a value of  for baselines longer than
the effective switching length
for baselines longer than
the effective switching length  (Holdaway and Owen, 1995).
Since the decorrelation is baseline dependent under fast switching,
the decorrelation correction methods described above would be helpful.
(Holdaway and Owen, 1995).
Since the decorrelation is baseline dependent under fast switching,
the decorrelation correction methods described above would be helpful.
Currently, it is believed that reasonable imaging with the 40 element
mma should be possible with 30 degree rms phase errors, assuming the
phase errors do not maintain some systematic value over long times.
The 30 degree rms phase error per baselines specification comes from
point source simulations (dynamic range = 200:1; Holdaway, 1992) and
from sensitivity arguments (down to 0.87). These simulations show
that the MMA will be able to make high fidelity, moderate dynamic
range images of complex sources with rms phase errors of 70 degrees per
baseline (the worst baselines in this simulation actually had rms
phase errors of 100 degrees). The 70 degree phase errors will result in a
stiff penalty in sensitivity since the decorrelation is down to 0.47
on the typical baseline. A modest resolution loss of 17% also
occurs.
We propose that we have two levels of phase error specifications:
- The primary phase error specification of 30 degrees rms
per baseline will permit excellent imaging with almost
no loss in sensitivity from decorrelation. This should
be the primary goal of our phase correction schemes.
- The secondary phase error specification of 70 degrees rms
per baseline will still permit very good imaging with a loss
of 50% in sensitivity (a factor of four in time). This
secondary phase error specification reminds us that
atmospheric conditions which do not allow us to meet the
primary phase error specification are not lost.
This will be particularly important for an instrument
which is built on a suboptimal site and for observations
at very high frequencies.
In Table 4 we explore what the 30 degree and 70 degree phase error
specifications mean for observing on a 300 m baseline at Chajnantor in
Chile without any phase calibration. We list the phase
stability quartiles measured on the NRAO 300 m, 11.2 GHz site test
interferometer for the month of June 1995, and then determine what
frequency can be observed with 30 degree and 70 degree phase errors. Fast
switching can achieve an effective calibration baseline 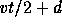 of
about 50 m (Holdaway and Owen, 1995), and typical phase structure
function power law exponents are 0.7, so the post-calibration phase
errors would be
of
about 50 m (Holdaway and Owen, 1995), and typical phase structure
function power law exponents are 0.7, so the post-calibration phase
errors would be 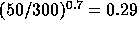 lower than the rms phase
errors measured on the 300 m baseline. These lower phase errors would
pertain to all baselines longer than 50 m, and would boost the peak
observing frequencies given in Table 4 by a factor of 3.5.
lower than the rms phase
errors measured on the 300 m baseline. These lower phase errors would
pertain to all baselines longer than 50 m, and would boost the peak
observing frequencies given in Table 4 by a factor of 3.5.



Next: Acknowledgements
Up: Correcting for Decorrelation Due
Previous: Comparing the Methods
 for short baselines
for short baselines 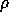 and saturate at
a value of
and saturate at
a value of  for baselines longer than
the effective switching length
for baselines longer than
the effective switching length  (Holdaway and Owen, 1995).
Since the decorrelation is baseline dependent under fast switching,
the decorrelation correction methods described above would be helpful.
(Holdaway and Owen, 1995).
Since the decorrelation is baseline dependent under fast switching,
the decorrelation correction methods described above would be helpful.
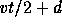 of
about 50 m (Holdaway and Owen, 1995), and typical phase structure
function power law exponents are 0.7, so the post-calibration phase
errors would be
of
about 50 m (Holdaway and Owen, 1995), and typical phase structure
function power law exponents are 0.7, so the post-calibration phase
errors would be 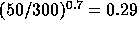 lower than the rms phase
errors measured on the 300 m baseline. These lower phase errors would
pertain to all baselines longer than 50 m, and would boost the peak
observing frequencies given in Table 4 by a factor of 3.5.
lower than the rms phase
errors measured on the 300 m baseline. These lower phase errors would
pertain to all baselines longer than 50 m, and would boost the peak
observing frequencies given in Table 4 by a factor of 3.5.