


Next: Correcting for Decorrelation
Up: Correcting for Decorrelation Due
Previous: Correcting for Decorrelation Due
Atmospheric phase errors cause trouble for millimeter interferometers:
systematic phase errors result in gross positional errors; systematic
and random phase errors limit the image quality; random phase errors
limit the sensitivity through decorrelation of the visibilities; time
dependent decorrelation results in flux scale errors; and since the
phase errors (and hence decorrelation) grow worse with baseline,
atmospheric phase errors limit the possible resolution of an array.
The best line of defense against this tropospheric menace is to avoid
the issue entirely by observing on a good site, on short baselines or
at low frequencies where the phase errors will be lower. Since the
science demands observations on long baselines and at high
frequencies, we are pushed to use an active phase calibration
technique which limits the residual phase errors to an acceptably low
level. We have written about a specification of 30 degree rms residual
phase error per baseline for any such exotic phase calibration
technique (Holdaway, 1992). We think the strongest justification for
this specification is the amplitude loss due to decorrelation given by
 (Thompson, Moran, and Swenson, 1986), where
(Thompson, Moran, and Swenson, 1986), where 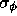 is the rms phase error per visibility in radians.
Hence, 30 degree rms phase errors will decrease the amplitude of the
visibilities by 0.87. If the time scale of the phase fluctuations is
larger than the integration time, the image flux will be down by 0.87,
and the phase fluctuations will scatter flux through the image.
However, this 13% loss in sensitivity is fairly modest, and we would
probably be willing to live with a higher loss in sensitivity if we
were performing exploratory observations at very high frequencies and
we could somehow correct for the effects of the decorrelation.
Hence, we should ask what level of phase errors will still permit
reasonable imaging, and can anything be done to correct for the image
errors caused by baseline dependent decorrelation?
is the rms phase error per visibility in radians.
Hence, 30 degree rms phase errors will decrease the amplitude of the
visibilities by 0.87. If the time scale of the phase fluctuations is
larger than the integration time, the image flux will be down by 0.87,
and the phase fluctuations will scatter flux through the image.
However, this 13% loss in sensitivity is fairly modest, and we would
probably be willing to live with a higher loss in sensitivity if we
were performing exploratory observations at very high frequencies and
we could somehow correct for the effects of the decorrelation.
Hence, we should ask what level of phase errors will still permit
reasonable imaging, and can anything be done to correct for the image
errors caused by baseline dependent decorrelation?



Next: Correcting for Decorrelation
Up: Correcting for Decorrelation Due
Previous: Correcting for Decorrelation Due
 (Thompson, Moran, and Swenson, 1986), where
(Thompson, Moran, and Swenson, 1986), where 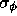 is the rms phase error per visibility in radians.
Hence, 30 degree rms phase errors will decrease the amplitude of the
visibilities by 0.87. If the time scale of the phase fluctuations is
larger than the integration time, the image flux will be down by 0.87,
and the phase fluctuations will scatter flux through the image.
However, this 13% loss in sensitivity is fairly modest, and we would
probably be willing to live with a higher loss in sensitivity if we
were performing exploratory observations at very high frequencies and
we could somehow correct for the effects of the decorrelation.
Hence, we should ask what level of phase errors will still permit
reasonable imaging, and can anything be done to correct for the image
errors caused by baseline dependent decorrelation?
is the rms phase error per visibility in radians.
Hence, 30 degree rms phase errors will decrease the amplitude of the
visibilities by 0.87. If the time scale of the phase fluctuations is
larger than the integration time, the image flux will be down by 0.87,
and the phase fluctuations will scatter flux through the image.
However, this 13% loss in sensitivity is fairly modest, and we would
probably be willing to live with a higher loss in sensitivity if we
were performing exploratory observations at very high frequencies and
we could somehow correct for the effects of the decorrelation.
Hence, we should ask what level of phase errors will still permit
reasonable imaging, and can anything be done to correct for the image
errors caused by baseline dependent decorrelation?