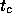(the lag time at which
the turnover occurs) by
M.A. Holdaway
National Radio Astronomy Observatory
July 6, 1995
Abstract
MMA Memo 129 (Holdaway, et al. 1995) introduced the basic data reduction pathway for the NRAO site test interferometers. One of the secondary data products derived in Memo 129 was the velocity of the water vapor aloft. We demonstrate two quite independent methods of measuring the wind velocity aloft agree to 5-10%.
Wind Velocity Aloft
In MMA Memo 129 (Holdaway, et al. 1995), we showed one method of
determining the mean horizontal velocity of the part of the atmosphere
which bears the turbulent water vapor, referred to below as the
velocity aloft. The temporal structure function of the interferometer
phase rises with lag time for times which are short compared to the
crossing time and then saturates or turns over for lag times which are
long compared to the crossing time. The velocity aloft v is related
to the baseline B and the ``corner time'' 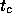(the lag time at which
the turnover occurs) by
where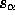 
is a scale factor which depends upon the structure
function exponent. We have determined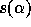 
empirically from
atmospheric simulations, and it is found to vary between 0.65 and 1.11
over the observed range in 
. Figure 7 of MMA Memo 129 shows a
time series of the velocity aloft and the surface wind velocity. The
apparent scatter in the velocity aloft led us to estimate its accuracy
at about 30%, but some larger systematic errors also seemed to affect the
velocity aloft. We indicated that some scatter might be expected since the
wind velocity generally increases with height and the water vapor
exists over a range of heights.
Another way to determine the velocity aloft is by comparing the temporal and spatial structure functions. Under the frozen screen model, temporal phase fluctuations are due to the spatial fluctuations passing overhead with velocity v (Treuhaft and Lanyi, 1987). Then the temporal and spatial structure functions are related:
Assuming a power law describes the structure functions accurately,
as the exponent of the spatial and temporal structure functions are the same. The velocity aloft is
With a single baseline interferometer, we can obtain the temporal
structure function of the interferometer phase, which is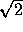 
times larger than the single point temporal structure function
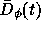. The interferometer also measures a single point
on the spatial phase structure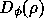 
at 
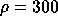m;
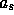can be determined from the 300 m point and the temporal
structure function exponent. If the structure function exponent
flattens on scales less than 300 m, the calculated velocity will be
larger than the true velocity. This method does not rely on any
simulations or complicated fitting techniques, and should be very
accurate if the constant power law assumption is met.
In Figure 1, we compare the velocity aloft calculated from the
temporal structure function turnover with the velocity aloft
calculated from the scaling between the temporal and the spatial
fluctuations from Chile site test data, 1995 May 10-26. The
correlation is very tight. The best fit line is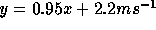 
with an rms of 1.2
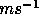about this line. The
excellent agreement in the velocity aloft as determined the two
different methods indicates that either method is in error by at most
5-10%, much better than we previously estimated. Fluctuations of the
velocity aloft over 20 minutes (see Figure 7 of MMA Memo 129) are much
larger than the estimated error in the velocity aloft. We need to use
shorter time series to properly sample the velocity aloft.
There are no instances of the velocity calculated from the temporal-spatial structure function scaling being much larger than the velocity calculated from the temporal structure function turnover, indicating the structure function exponent is fairly constant up to 300 m. The constancy of the structure function exponent out to 300 m is indirect evidence for a thick (>300 m) screen of turbulent water vapor.
In Figure 2, we compare the surface wind velocity and the velocity aloft calculated from the temporal structure function turnover. The velocity aloft is nearly always larger than the surface velocity.
References
Holdaway, M.A., Radford, Simon J.E. , Owen, F.N., and Foster, Scott M., 1995, MMA Memo 129, ``Data Processing for Site Test Interferometers''.
Treuhaft, Lanyi 1987, ``The Effect of the dynamic wet troposphere on radio interferometric measurements,'' Radio Science, Vol 22, No 2, 251-265.
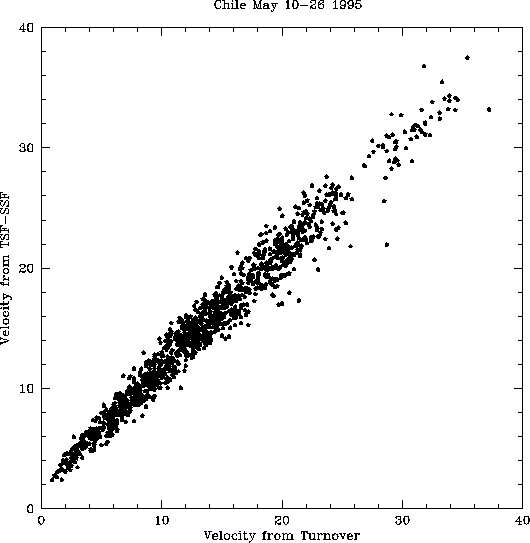
Figure 1: Derived velocity of the winds aloft as
calculated from the scaling between the spatial and temporal
structure functions, plotted against the velocity calculated from the
temporal structure function turnover and simulations.
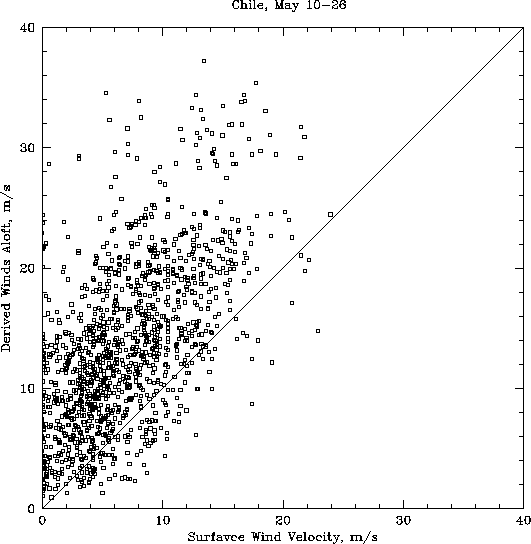
Figure 2: Derived velocity of the winds aloft as
calculated from the scaling between the spatial and temporal
structure functions, plotted against the surface wind velocity
measured at our weather station.
This document was generated using the LaTeX2HTML translator Version 95 (Thu Jan 19 1995) Copyright © 1993, 1994, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 velocity.tex.
The translation was initiated by Mark Holdaway on Tue Sep 5 15:23:40 MDT 1995