Return to Memolist
MMA Memo 129: Data Processing for Site Test Interferometers
M.A. Holdaway, Simon J.E. Radford, F.N. Owen, and Scott M. Foster
National Radio Astronomy Observatory
June 27, 1995
Abstract
The NRAO site test interferometers measure atmospheric path length
fluctuations on a 300 m baseline. Here we describe data products
derived from those measurements that can be used for site
intercomparison and atmospheric modeling. As a demonstration of this
analysis, we have processed two weeks of data from the instrument in
Chile for 1995 May.
Introduction
To further evaluate possible sites for the MMA, NRAO has installed two
site test interferometers, one at the VLBA site at 3720 m on Mauna
Kea and the other at 5000 m near Cerro Chajnantor in northern Chile
(near San Pedro de Atacama). These interferometers observe
geostationary satellites to measure path length fluctuations due to
inhomogeneously distributed water vapor. Unless they can be calibrated
on short time scales, such fluctuations are a fundamental limit to the
angular resolution of observations at millimeter and submillimeter
wavelengths. From these measurements we wish to characterize the
temporal and spatial variations of the path length, to estimate the
natural seeing limits at given frequencies, and to estimate residual
phase errors associated with a variety of phase calibration
schemes. This information will ultimately be used to select the best
site.
Interferometer and Phase Time Series
Each interferometer (Radford et al. 1995) has two 1.8 m antennas
separated by 300 m. On Mauna Kea, the interferometer observes an
unmodulated beacon at 11.7269 GHz on Gstar4 (105 W longitude,
29
W longitude,
29 elevation) and at Cerro Chajnantor, the instrument observes a
11.198 GHz beacon on Intelsat 601 (27.5
elevation) and at Cerro Chajnantor, the instrument observes a
11.198 GHz beacon on Intelsat 601 (27.5 W longitude, 36
W longitude, 36 elevation). The power signal-to-noise ratio is 65 dB Hz
elevation). The power signal-to-noise ratio is 65 dB Hz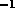 on
Mauna Kea and 58 dB Hz
on
Mauna Kea and 58 dB Hz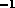 at Cerro Chajnantor. The received
signals are amplified, downconverted, and transmitted to a central
station, where they are further downconverted and the signal from one
antenna is phase locked to the satellite beacon. These signals are
then filtered, downconverted to 5 kHz, and digitized at
20 ksamples sec
at Cerro Chajnantor. The received
signals are amplified, downconverted, and transmitted to a central
station, where they are further downconverted and the signal from one
antenna is phase locked to the satellite beacon. These signals are
then filtered, downconverted to 5 kHz, and digitized at
20 ksamples sec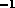 . The digital streams are multiplied and
averaged for 1 s to extract the relative phase of the signals and the
phase time series is written to a file in 60 s blocks along with
engineering data. Graphical summaries of the data and of the
instrument performance are faxed to our offices once or twice daily.
The raw data are copied to tape and retrieved every month or two.
Each block of sixty 1 s phases is perfectly synchronous, i. e., no
samples are lost, and the gaps between the blocks are a few
. The digital streams are multiplied and
averaged for 1 s to extract the relative phase of the signals and the
phase time series is written to a file in 60 s blocks along with
engineering data. Graphical summaries of the data and of the
instrument performance are faxed to our offices once or twice daily.
The raw data are copied to tape and retrieved every month or two.
Each block of sixty 1 s phases is perfectly synchronous, i. e., no
samples are lost, and the gaps between the blocks are a few 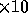 ms. This time series is the starting point for the analysis
described here.
ms. This time series is the starting point for the analysis
described here.
Desired Data Products
The primary data products that can be determined from
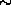 10 minute segments of the interferometer phase
time series include:
10 minute segments of the interferometer phase
time series include:
We can also construct some derived data products from these primary
data products. These include:
Finally, the database of primary data products can be joined with the
opacity database and the weather station database. The resulting
joint database will provide many correlational data products
that can be important diagnostics for understanding the dynamics of
the atmosphere (Holdaway, Ishiguro, and Morita 1995).
Analysis of the phase time series and generation of the primary and
derived data products require both new software and some
experimentation. This memo documents our current view of the data
processing used to obtain the primary data products. Analysis of
correlations in the final joint database must wait until there is a
substantial amount of site data from which we can draw statistical
conclusions.
Data Calibration
An interferometer will detect atmospheric fluctuations on time scales
ranging from 0 to a few times 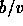 , where b is the physical
baseline. Radiosonde measurements indicate typical winds aloft are
5 m s
, where b is the physical
baseline. Radiosonde measurements indicate typical winds aloft are
5 m s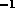 above Mauna Kea (Schwab 1992) and 10 m s
above Mauna Kea (Schwab 1992) and 10 m s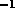 above
Cerro Chajnantor (Schwab private communication), so crossing
times are 30 to 60 s. The phase structure function is the variance of
the phase as a function of baseline, calculated over many atmospheric
instantiations, usually approximated as many crossing times. The site
test interferometer directly measures the phase structure function on
a single 300 m baseline, and we require about 10 minutes of data to
ensure many crossing times. Determining the baseline crossing time,
which indicates the atmospheric velocity, also requires several
crossing times.
above
Cerro Chajnantor (Schwab private communication), so crossing
times are 30 to 60 s. The phase structure function is the variance of
the phase as a function of baseline, calculated over many atmospheric
instantiations, usually approximated as many crossing times. The site
test interferometer directly measures the phase structure function on
a single 300 m baseline, and we require about 10 minutes of data to
ensure many crossing times. Determining the baseline crossing time,
which indicates the atmospheric velocity, also requires several
crossing times.
On 10 minute time scales, however, there are significant phase
variations caused by satellite motion and thermal changes in the
instrument. These manifest themselves as gross, primarilly linear,
trends in the data. When the satellite motion changes direction, or
when temperature has a second time derivative, there can also be
curvature in the instrumental contribution to the phase. Examination
of the data indicates removal of a quadratic trend is sometimes
required. If satellite motion causes five turns of phase per 24
hours, then the rms phase about the mean over 1024 s1 would be inflated by as much as 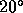 . Even
after removing a linear trend from a 1024 s series, satellite motion
could still contribute as much as
. Even
after removing a linear trend from a 1024 s series, satellite motion
could still contribute as much as 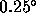 to the rms phase, which is
comparable to the expected atmospheric contribution during good
conditions. In fact, some data indicate if a quadratic term were not
removed, the rms phase over 1024 s would be inflated by as much as
to the rms phase, which is
comparable to the expected atmospheric contribution during good
conditions. In fact, some data indicate if a quadratic term were not
removed, the rms phase over 1024 s would be inflated by as much as
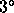 , much more than can be explained by the satellite motion. These
data are probably affected by thermal drifts of the instrument. If a
quadratic trend is fit over the 1024 s, however, satellite motion can
contribute no more than
, much more than can be explained by the satellite motion. These
data are probably affected by thermal drifts of the instrument. If a
quadratic trend is fit over the 1024 s, however, satellite motion can
contribute no more than 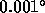 to the rms phase, which is
substantially less than the interferometer sensitivity or the best
atmospheric conditions. Finally, subtracting a quadratic fit over a
suitably long time will not alter the atmospheric phase fluctuations
significantly. Simulations with typical power law exponents for the
structure function indicate removing a quadratic trend from the 1024 s phase
time series removes only about 1% of the atmospheric phase
fluctuations.
to the rms phase, which is
substantially less than the interferometer sensitivity or the best
atmospheric conditions. Finally, subtracting a quadratic fit over a
suitably long time will not alter the atmospheric phase fluctuations
significantly. Simulations with typical power law exponents for the
structure function indicate removing a quadratic trend from the 1024 s phase
time series removes only about 1% of the atmospheric phase
fluctuations.
In the presence of significant instrumental phase noise, the power
spectrum of the interferometer phase is ill behaved at high
frequencies. Hence, only those lower frequencies where the atmospheric
phase fluctuations are much higher than the instrumental phase jitter
can be used to estimate the phase structure function exponent. In
addition, it is not at all straightforward to remove the instrumental
power spectrum from the measured power spectrum. Holdaway, Ishiguro,
and Morita (1995) demonstrate, however, the spatial phase structure
function can be determined from the temporal structure function of the
interferometer phase. Indeed this is sometimes better than using the
power spectrum. For times shorter than the crossing time, the
temporal structure function of the interferometer phase,
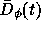 , is related to the spatial structure function,
, is related to the spatial structure function,
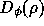 , as
, as

Furthermore, the temporal structure function is well behaved in the
presence of instrumental noise. The temporal structure function
of the instrumental phase can be removed from the temporal structure
function of the measured phase by simple differencing,
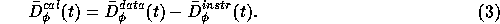
In terms of the rms phase of the time series,
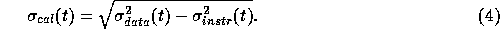
Simulations indicate that even after an instrumental term up to 5
times larger than the atmospheric phase fluctuations has been removed,
the structure function exponent and the rms atmospheric phase can
still be determined to an accuracy of about 20%. To demonstrate
these concepts, Figure 1 shows the power spectrum of a
phase time series from Chile that appears to be limited by white
instrumental phase noise, and Figure 2 shows the
temporal phase structure function of the same time series, both before
and after the instrumental term has been subtracted.
During the best conditions on Mauna Kea, we have not seen any times
when instrumental phase noise obviously contributes to the structure
function (and hence to the rms phase). At the summit, the best phase
conditions measured on a 100 m baseline are about 0.1 degree rms at
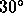 elevation, uncorrected for airmass effects (Masson, 1993).
This scales to 0.23 degrees rms for a 300 m baseline if the structure
function exponent is 0.75, the median value. These data are
consistent with the lowest rms phases we measure at the VLBA site.
The structure function exponent,
elevation, uncorrected for airmass effects (Masson, 1993).
This scales to 0.23 degrees rms for a 300 m baseline if the structure
function exponent is 0.75, the median value. These data are
consistent with the lowest rms phases we measure at the VLBA site.
The structure function exponent,  , does tend however toward
low values during the best phase conditions. This implies either
the phase is dominated by water vapor in a thin screen or that
, does tend however toward
low values during the best phase conditions. This implies either
the phase is dominated by water vapor in a thin screen or that
 is artificially flattened by instrumental noise on short time
scales. We are still looking for an instrumental term in the Mauna
Kea data, but until we find clear evidence, we do not plan to subtract
any instrumental term from the data.
is artificially flattened by instrumental noise on short time
scales. We are still looking for an instrumental term in the Mauna
Kea data, but until we find clear evidence, we do not plan to subtract
any instrumental term from the data.
During the very best conditions on the Chilean site, on the other
hand, there is a clear indication of instrumental noise in the
temporal structure function. During those conditions, the square root
of the structure function on short time scales saturates at about
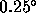 . Furthermore, we can iteratively subtract white noise from
the structure function until it no longer flattens out on the
shortest times. While the convergence rate varies for different data,
this process converges to a common white noise amplitude of
. Furthermore, we can iteratively subtract white noise from
the structure function until it no longer flattens out on the
shortest times. While the convergence rate varies for different data,
this process converges to a common white noise amplitude of 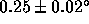 rms. When we subtract this noise from the phase structure
functions, we find the power law fit stays reasonable down to
1-2 seconds. There may still be residual instrumental phase noise in
the structure function at the level of
rms. When we subtract this noise from the phase structure
functions, we find the power law fit stays reasonable down to
1-2 seconds. There may still be residual instrumental phase noise in
the structure function at the level of 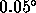 rms, but this is
much lower than the best atmospheric conditions and does not affect
the structure function exponent.
rms, but this is
much lower than the best atmospheric conditions and does not affect
the structure function exponent.
The 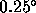 rms white noise in the temporal structure function of the
interferometer phase corresponds to
rms white noise in the temporal structure function of the
interferometer phase corresponds to 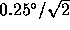 white noise in
the measured phase time series. Hence, we subtract
white noise in
the measured phase time series. Hence, we subtract 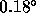 in
quadrature from the rms phases to obtain the final calibrated value.
in
quadrature from the rms phases to obtain the final calibrated value.
Primary Data Products
RMS Phase. The single most useful piece of information is the
rms phase calculated for a time long compared to the crossing time,
after the gross trends and phase noise have been removed. The
cumulative distribution of the calibrated rms phase at 11.2 GHz on a
300 m baseline for May 10-26 on the Chile site is shown in
Figure 3. For easy comparison with the SMA archive
of data for Mauna Kea, we have converted this to microns of path
length on a 100 m baseline using the structure function exponents
derived below (Figure 4). The satellite elevation
is 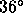 , or 1.7 airmasses. Holdaway and Ishiguro (1995) and
Treuhaft and Lanyi (1987) indicate that for short baselines (i.e.,
300 m), the phase errors scale with the square root of the airmass.
Hence to estimate the zenith path length fluctuations, we divide the
measured fluctuations by 1.3.
, or 1.7 airmasses. Holdaway and Ishiguro (1995) and
Treuhaft and Lanyi (1987) indicate that for short baselines (i.e.,
300 m), the phase errors scale with the square root of the airmass.
Hence to estimate the zenith path length fluctuations, we divide the
measured fluctuations by 1.3.
Phase Structure Function Exponent. As indicated above, the
exponent of the power law fit to the temporal structure function of
the interferometer phase should be equal to the power law exponent of
the spatial phase structure function. It is crucial to subtract the
instrumental phase noise from the temporal structure function before
fitting the power law. Otherwise, the noise will inflate the rms
phase on short times during good conditions and lower  by
0.1-0.3. We estimate residual instrumental noise is less than
by
0.1-0.3. We estimate residual instrumental noise is less than
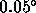 rms, which will lower
rms, which will lower  only about 0.01 under the best
atmospheric conditions. To avoid the affects of the residual
instrumental noise, we ignore the 1 s point in fitting the exponent.
The temporal structure function of the interferometer phase will also
turn over at times comparable to the crossing time, so we must also
include an upper time limit when fitting the power law. This upper
limit is determined iteratively (see below).
only about 0.01 under the best
atmospheric conditions. To avoid the affects of the residual
instrumental noise, we ignore the 1 s point in fitting the exponent.
The temporal structure function of the interferometer phase will also
turn over at times comparable to the crossing time, so we must also
include an upper time limit when fitting the power law. This upper
limit is determined iteratively (see below).
In Figure 5 we show the structure function exponent
plotted against the rms phase, before and after subtracting the noise.
Even after correcting for the instrumental noise,  still
decreases somewhat during the lowest rms phase conditions. While this
could be caused by residual instrumental noise, our estimates of any
residual instrumental effect are consistent with a true decrease of
the structure function exponent. This is also seen at Nobeyama
(Holdaway, Ishiguro, and Morita 1995), where the instrumental function
is smaller and the atmospheric phase fluctuations are larger.
Exponents intermediate between the Kolmogorov values of 0.83 for a
thick atmosphere and 0.33 for a thin atmosphere can be obtained from a
superposition of a thick and a thin layer. Hence during the very good
conditions in Chile, most of the turbulent water vapor seems to be in
a thin (
still
decreases somewhat during the lowest rms phase conditions. While this
could be caused by residual instrumental noise, our estimates of any
residual instrumental effect are consistent with a true decrease of
the structure function exponent. This is also seen at Nobeyama
(Holdaway, Ishiguro, and Morita 1995), where the instrumental function
is smaller and the atmospheric phase fluctuations are larger.
Exponents intermediate between the Kolmogorov values of 0.83 for a
thick atmosphere and 0.33 for a thin atmosphere can be obtained from a
superposition of a thick and a thin layer. Hence during the very good
conditions in Chile, most of the turbulent water vapor seems to be in
a thin (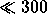 m) layer. This may be the boundary of the inversion
layer that often forms 500-1000 m above that site. In the
distribution of
m) layer. This may be the boundary of the inversion
layer that often forms 500-1000 m above that site. In the
distribution of  (Figure 6), note the sharp
cutoff near 0.83 and the more gradual approach to 0.33. The
distribution of
(Figure 6), note the sharp
cutoff near 0.83 and the more gradual approach to 0.33. The
distribution of  and the relationship between
and the relationship between  and rms
phase suggest there is an everpresent thin turbulent water vapor
layer and a thick turbulent water vapor layer of variable strength that
dominates the phase in all but the best conditions.
and rms
phase suggest there is an everpresent thin turbulent water vapor
layer and a thick turbulent water vapor layer of variable strength that
dominates the phase in all but the best conditions.
``Corner Time'' and Velocity Aloft. The corner time, 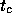 ,
analogous to Masson's (1993) corner frequency, is the time scale
where the phase structure function turns over. We determine it
iteratively: we fit a power law to the temporal phase structure
function between 2 and 15 s time scales and find the mean phase
between 50 and 300 second time scales. Unlike the power spectrum, the
temporal phase structure function is (approximately) flat at long
times. The time where the two fits intersect determines the new upper
limit for the power law fit to the short time scales and the new lower
limit for the mean of the long time scales. This process usually
converges in three iterations. The corner time can be related to the
crossing time of the array, and hence to the velocity, by atmospheric
simulations (i.e., similar to Holdaway, Ishiguro, and Morita 1995).
Simulations of atmospheres with velocities of 5-20 m
,
analogous to Masson's (1993) corner frequency, is the time scale
where the phase structure function turns over. We determine it
iteratively: we fit a power law to the temporal phase structure
function between 2 and 15 s time scales and find the mean phase
between 50 and 300 second time scales. Unlike the power spectrum, the
temporal phase structure function is (approximately) flat at long
times. The time where the two fits intersect determines the new upper
limit for the power law fit to the short time scales and the new lower
limit for the mean of the long time scales. This process usually
converges in three iterations. The corner time can be related to the
crossing time of the array, and hence to the velocity, by atmospheric
simulations (i.e., similar to Holdaway, Ishiguro, and Morita 1995).
Simulations of atmospheres with velocities of 5-20 m 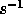 and
structure function exponents of 0.37-0.73 indicate tthe scaling
between
and
structure function exponents of 0.37-0.73 indicate tthe scaling
between 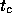 and atmospheric velocity v depends upon the
structure function exponent,
and atmospheric velocity v depends upon the
structure function exponent,

where b is the nonprojected baseline, and
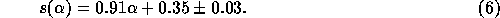
The uncertainty is estimated from the scatter in the simulations. To
demonstrate the derived wind velocity aloft is actually measuring
something, we provide a time series of the derived wind aloft and
compare it to the measured surface wind velocity
(Figure 7). The scatter in the derived wind aloft
indicates there are probably some systematic errors causing
uncertainties of more than a factor of 2 (see the scatter around time
= 21.2), but also there are times when the scatter in the derived
velocity is as low as 30% (see time = 20.8). Since the velocity of
the winds aloft is a strong function of altitude and the
interferometer samples the velocity at all altitudes where turbulent
water vapor exists, we do not expect an unambiguous result. We are still
investigating other possible means of estimating the wind velocity
aloft from the interferometer phase time series.
Software Development
The data calibration, reduction, and analysis has been prototyped
using UNIX shell scripts, SM, and SDE (Cornwell, Briggs, and Holdaway,
1995). Rather than using this heterogeneous assortment of software
for the production data reduction, we plan to add the analysis to the
data acquisition software, which is written with LabView. We will
then calculate the primary data products for each 1024 s period at the
site. A table of these statistics will be small enough to be
transmitted daily by telephone.
References
Cornwell, T.J., Briggs, D.S., and Holdaway, M.A., 1995,
SDE Users Guide.
Holdaway, M.A., and Ishiguro, Masato, 1995, MMA Memo 127,
``Dependence of Tropospheric Path Length Fluctuations on Airmass.''
Holdaway, M.A., Ishiguro, Masato, and Morita, K.-I., 1995, MMA Memo ???,
``Analysis of the Spatial and Temporal Phase Fluctuations Above
Nobeyama.''
Masson, C.R., 1994, ``Atmospheric Effects and Calibration'',
in Astronomy with Millimeter and Submillimeter Wave
Interferometry, eds. Ishiguro and Welch.
Radford, S.J.E., et al., 1995, in preparation.
Schwab, F., 1992, MMA Memo 75, ``Lower Tropospheric Wind Speeds.....''.
Tatarski, V.I., 1961, Wave Propagation in a Turbulent Medium,
McGraw-Hill, New York.
Treuhaft, Lanyi 1987, ``The Effect of the dynamic wet troposphere on
radio interferometric measurements,'' Radio Science, Vol 22, No 2,
251-265.
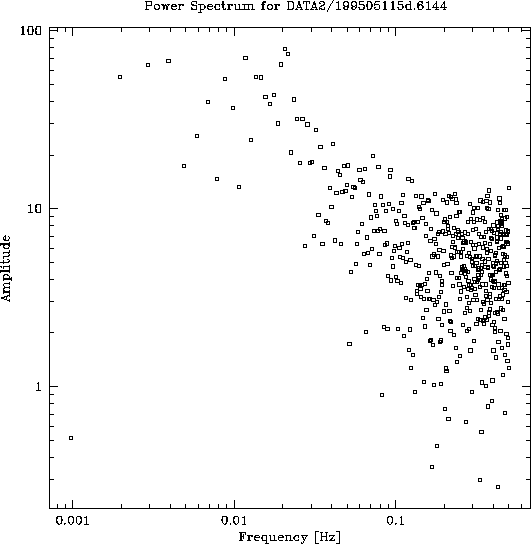
Figure 1: How instrumental phase noise
affects the interferometer data: the square root of the power
spectrum of a phase time series that is limited by white instrumental
phase noise. The high frequencies are so corrupted by noise that a
valid slope cannot be fit to the atmospheric fluctuations, and a
turnover indicative of the atmospheric velocity is hard to
discern. The power spectrum is also too poorly behaved to be able to
remove an instrumental function.
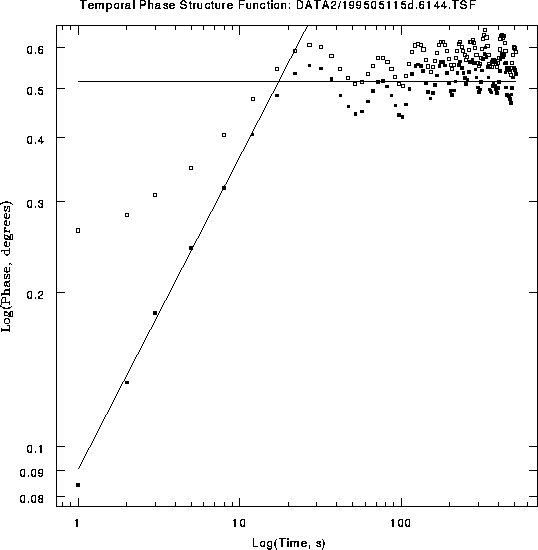
Figure 2: How instrumental phase noise affects the interferometer
data: the square root of the temporal structure function of the same
time series, both before the instrumental noise is removed (open
squares) and after 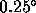 rms white noise is subtracted (filled
squares). The sloping line is the fit to the atmospheric
fluctuations and has a slope of
rms white noise is subtracted (filled
squares). The sloping line is the fit to the atmospheric
fluctuations and has a slope of  . The intersection of the
two lines defines the ``corner time''
. The intersection of the
two lines defines the ``corner time'' 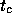 . The oscillations on
long times are probably an indication of the atmospheric velocity,
but we have not yet exploited this information.
. The oscillations on
long times are probably an indication of the atmospheric velocity,
but we have not yet exploited this information.
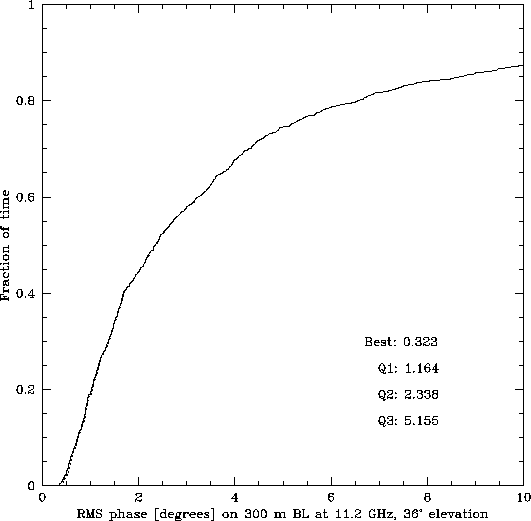
Figure: Cumulative distribution of rms
phase in degrees at 11.2 GHz on a 300m baseline for 1995 May 10-26 on
the Chile site. The satellite elevation is 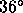 , so zenith
fluctuations would be about 1.3 times lower.
, so zenith
fluctuations would be about 1.3 times lower.
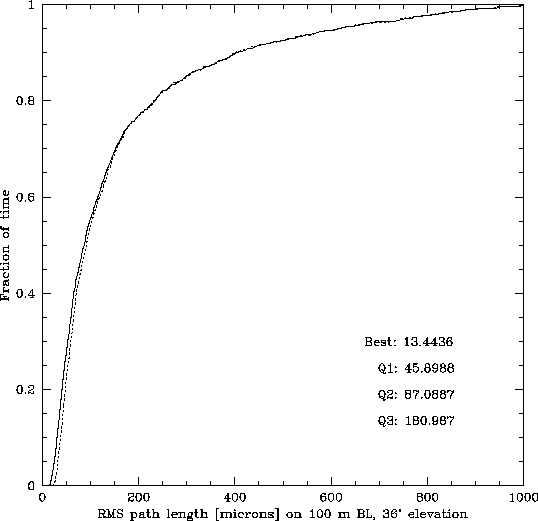
Figure 4: Cumulative
distribution of rms path length in microns estimated for a 100m
baseline for May 10-26 on the Chile site. The data have not been
corrected to the zenith. The solid curve is the rms phase after the
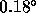 white noise has been subtracted, and the dashed curve is
without calibration.
white noise has been subtracted, and the dashed curve is
without calibration.
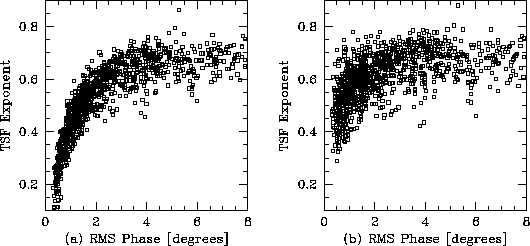
Figure 5: Structure function exponent  plotted against the rms phase
(a) prior to removing the instrumental
term, and (b) after variance subtraction of a
plotted against the rms phase
(a) prior to removing the instrumental
term, and (b) after variance subtraction of a 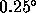 white noise.
Data for 1995 May 10-26 on the Chile site.
white noise.
Data for 1995 May 10-26 on the Chile site.
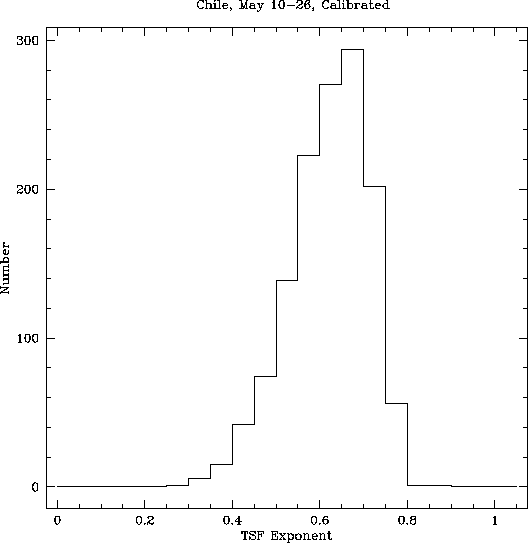
Figure 6: Distribution of the structure function exponent  for 1995 May 10-26 on the Chile site.
for 1995 May 10-26 on the Chile site.
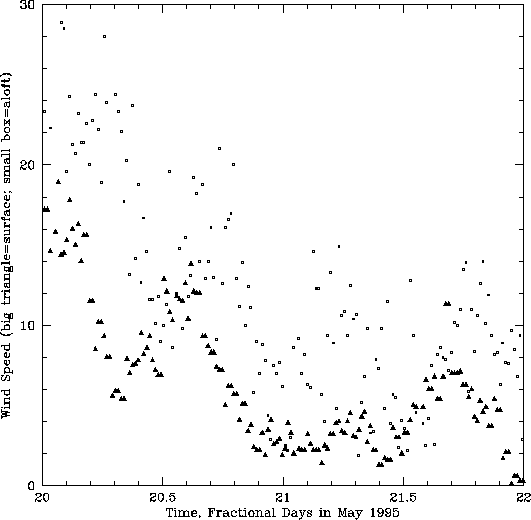
Figure 7: Derived velocity of the winds aloft as a function of time
(small boxes) and measured surface wind velocity as a function of time
(large triangles) for 1995 May 20-22 on the Chile site.
...s Although
powers of two have no special meaning for calculating the phase
structure function, we have continued with a 1024 s time series in
this memo as a vestage of using the power spectrum to determine the
structure function exponent. Using the temporal structure function to
determine the structure function exponent will allow a shorter time
series, perhaps 600 s.
 W longitude,
29
W longitude,
29 elevation) and at Cerro Chajnantor, the instrument observes a
11.198 GHz beacon on Intelsat 601 (27.5
elevation) and at Cerro Chajnantor, the instrument observes a
11.198 GHz beacon on Intelsat 601 (27.5 W longitude, 36
W longitude, 36 elevation). The power signal-to-noise ratio is 65 dB Hz
elevation). The power signal-to-noise ratio is 65 dB Hz on
Mauna Kea and 58 dB Hz
on
Mauna Kea and 58 dB Hz at Cerro Chajnantor. The received
signals are amplified, downconverted, and transmitted to a central
station, where they are further downconverted and the signal from one
antenna is phase locked to the satellite beacon. These signals are
then filtered, downconverted to 5 kHz, and digitized at
20 ksamples sec
at Cerro Chajnantor. The received
signals are amplified, downconverted, and transmitted to a central
station, where they are further downconverted and the signal from one
antenna is phase locked to the satellite beacon. These signals are
then filtered, downconverted to 5 kHz, and digitized at
20 ksamples sec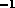 . The digital streams are multiplied and
averaged for 1 s to extract the relative phase of the signals and the
phase time series is written to a file in 60 s blocks along with
engineering data. Graphical summaries of the data and of the
instrument performance are faxed to our offices once or twice daily.
The raw data are copied to tape and retrieved every month or two.
Each block of sixty 1 s phases is perfectly synchronous, i. e., no
samples are lost, and the gaps between the blocks are a few
. The digital streams are multiplied and
averaged for 1 s to extract the relative phase of the signals and the
phase time series is written to a file in 60 s blocks along with
engineering data. Graphical summaries of the data and of the
instrument performance are faxed to our offices once or twice daily.
The raw data are copied to tape and retrieved every month or two.
Each block of sixty 1 s phases is perfectly synchronous, i. e., no
samples are lost, and the gaps between the blocks are a few 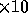 ms. This time series is the starting point for the analysis
described here.
ms. This time series is the starting point for the analysis
described here.
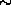 10 minute segments of the interferometer phase
time series include:
10 minute segments of the interferometer phase
time series include:
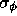 ,
and the exponent of a power law fit to the phase structure
function,
,
and the exponent of a power law fit to the phase structure
function,  . The phase structure function
. The phase structure function 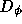 ,
is given by
,
is given by
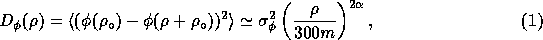
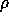 is the distance between two antennas and
is the distance between two antennas and 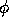 is the atmospheric phase. Given the phase structure function,
we can predict the rms phase on any baseline
shorter than the measured baseline and extrapolate to the
rms phase on longer baselines.
is the atmospheric phase. Given the phase structure function,
we can predict the rms phase on any baseline
shorter than the measured baseline and extrapolate to the
rms phase on longer baselines.

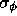 is the rms phase on a reference
baseline,
is the rms phase on a reference
baseline,  is the exponent of the phase structure
function power law (together
is the exponent of the phase structure
function power law (together 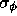 and
and  define the phase structure function), and v is the wind
velocity aloft. This information is required to determine how
well phase calibration techniques, such as fast switching or
paired antenna phase calibration, will work.
define the phase structure function), and v is the wind
velocity aloft. This information is required to determine how
well phase calibration techniques, such as fast switching or
paired antenna phase calibration, will work.
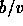 , where b is the physical
baseline. Radiosonde measurements indicate typical winds aloft are
5 m s
, where b is the physical
baseline. Radiosonde measurements indicate typical winds aloft are
5 m s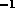 above Mauna Kea (Schwab 1992) and 10 m s
above Mauna Kea (Schwab 1992) and 10 m s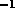 above
Cerro Chajnantor (Schwab private communication), so crossing
times are 30 to 60 s. The phase structure function is the variance of
the phase as a function of baseline, calculated over many atmospheric
instantiations, usually approximated as many crossing times. The site
test interferometer directly measures the phase structure function on
a single 300 m baseline, and we require about 10 minutes of data to
ensure many crossing times. Determining the baseline crossing time,
which indicates the atmospheric velocity, also requires several
crossing times.
above
Cerro Chajnantor (Schwab private communication), so crossing
times are 30 to 60 s. The phase structure function is the variance of
the phase as a function of baseline, calculated over many atmospheric
instantiations, usually approximated as many crossing times. The site
test interferometer directly measures the phase structure function on
a single 300 m baseline, and we require about 10 minutes of data to
ensure many crossing times. Determining the baseline crossing time,
which indicates the atmospheric velocity, also requires several
crossing times.
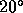 . Even
after removing a linear trend from a 1024 s series, satellite motion
could still contribute as much as
. Even
after removing a linear trend from a 1024 s series, satellite motion
could still contribute as much as 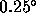 to the rms phase, which is
comparable to the expected atmospheric contribution during good
conditions. In fact, some data indicate if a quadratic term were not
removed, the rms phase over 1024 s would be inflated by as much as
to the rms phase, which is
comparable to the expected atmospheric contribution during good
conditions. In fact, some data indicate if a quadratic term were not
removed, the rms phase over 1024 s would be inflated by as much as
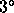 , much more than can be explained by the satellite motion. These
data are probably affected by thermal drifts of the instrument. If a
quadratic trend is fit over the 1024 s, however, satellite motion can
contribute no more than
, much more than can be explained by the satellite motion. These
data are probably affected by thermal drifts of the instrument. If a
quadratic trend is fit over the 1024 s, however, satellite motion can
contribute no more than 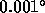 to the rms phase, which is
substantially less than the interferometer sensitivity or the best
atmospheric conditions. Finally, subtracting a quadratic fit over a
suitably long time will not alter the atmospheric phase fluctuations
significantly. Simulations with typical power law exponents for the
structure function indicate removing a quadratic trend from the 1024 s phase
time series removes only about 1% of the atmospheric phase
fluctuations.
to the rms phase, which is
substantially less than the interferometer sensitivity or the best
atmospheric conditions. Finally, subtracting a quadratic fit over a
suitably long time will not alter the atmospheric phase fluctuations
significantly. Simulations with typical power law exponents for the
structure function indicate removing a quadratic trend from the 1024 s phase
time series removes only about 1% of the atmospheric phase
fluctuations.
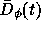 , is related to the spatial structure function,
, is related to the spatial structure function,
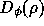 , as
, as

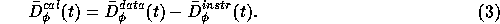
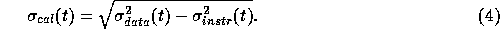
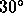 elevation, uncorrected for airmass effects (Masson, 1993).
This scales to 0.23 degrees rms for a 300 m baseline if the structure
function exponent is 0.75, the median value. These data are
consistent with the lowest rms phases we measure at the VLBA site.
The structure function exponent,
elevation, uncorrected for airmass effects (Masson, 1993).
This scales to 0.23 degrees rms for a 300 m baseline if the structure
function exponent is 0.75, the median value. These data are
consistent with the lowest rms phases we measure at the VLBA site.
The structure function exponent,  , does tend however toward
low values during the best phase conditions. This implies either
the phase is dominated by water vapor in a thin screen or that
, does tend however toward
low values during the best phase conditions. This implies either
the phase is dominated by water vapor in a thin screen or that
 is artificially flattened by instrumental noise on short time
scales. We are still looking for an instrumental term in the Mauna
Kea data, but until we find clear evidence, we do not plan to subtract
any instrumental term from the data.
is artificially flattened by instrumental noise on short time
scales. We are still looking for an instrumental term in the Mauna
Kea data, but until we find clear evidence, we do not plan to subtract
any instrumental term from the data.
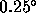 . Furthermore, we can iteratively subtract white noise from
the structure function until it no longer flattens out on the
shortest times. While the convergence rate varies for different data,
this process converges to a common white noise amplitude of
. Furthermore, we can iteratively subtract white noise from
the structure function until it no longer flattens out on the
shortest times. While the convergence rate varies for different data,
this process converges to a common white noise amplitude of 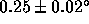 rms. When we subtract this noise from the phase structure
functions, we find the power law fit stays reasonable down to
1-2 seconds. There may still be residual instrumental phase noise in
the structure function at the level of
rms. When we subtract this noise from the phase structure
functions, we find the power law fit stays reasonable down to
1-2 seconds. There may still be residual instrumental phase noise in
the structure function at the level of 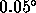 rms, but this is
much lower than the best atmospheric conditions and does not affect
the structure function exponent.
rms, but this is
much lower than the best atmospheric conditions and does not affect
the structure function exponent.
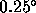 rms white noise in the temporal structure function of the
interferometer phase corresponds to
rms white noise in the temporal structure function of the
interferometer phase corresponds to 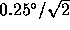 white noise in
the measured phase time series. Hence, we subtract
white noise in
the measured phase time series. Hence, we subtract 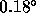 in
quadrature from the rms phases to obtain the final calibrated value.
in
quadrature from the rms phases to obtain the final calibrated value.
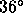 , or 1.7 airmasses. Holdaway and Ishiguro (1995) and
Treuhaft and Lanyi (1987) indicate that for short baselines (i.e.,
300 m), the phase errors scale with the square root of the airmass.
Hence to estimate the zenith path length fluctuations, we divide the
measured fluctuations by 1.3.
, or 1.7 airmasses. Holdaway and Ishiguro (1995) and
Treuhaft and Lanyi (1987) indicate that for short baselines (i.e.,
300 m), the phase errors scale with the square root of the airmass.
Hence to estimate the zenith path length fluctuations, we divide the
measured fluctuations by 1.3.
 by
0.1-0.3. We estimate residual instrumental noise is less than
by
0.1-0.3. We estimate residual instrumental noise is less than
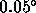 rms, which will lower
rms, which will lower  only about 0.01 under the best
atmospheric conditions. To avoid the affects of the residual
instrumental noise, we ignore the 1 s point in fitting the exponent.
The temporal structure function of the interferometer phase will also
turn over at times comparable to the crossing time, so we must also
include an upper time limit when fitting the power law. This upper
limit is determined iteratively (see below).
only about 0.01 under the best
atmospheric conditions. To avoid the affects of the residual
instrumental noise, we ignore the 1 s point in fitting the exponent.
The temporal structure function of the interferometer phase will also
turn over at times comparable to the crossing time, so we must also
include an upper time limit when fitting the power law. This upper
limit is determined iteratively (see below).
 still
decreases somewhat during the lowest rms phase conditions. While this
could be caused by residual instrumental noise, our estimates of any
residual instrumental effect are consistent with a true decrease of
the structure function exponent. This is also seen at Nobeyama
(Holdaway, Ishiguro, and Morita 1995), where the instrumental function
is smaller and the atmospheric phase fluctuations are larger.
Exponents intermediate between the Kolmogorov values of 0.83 for a
thick atmosphere and 0.33 for a thin atmosphere can be obtained from a
superposition of a thick and a thin layer. Hence during the very good
conditions in Chile, most of the turbulent water vapor seems to be in
a thin (
still
decreases somewhat during the lowest rms phase conditions. While this
could be caused by residual instrumental noise, our estimates of any
residual instrumental effect are consistent with a true decrease of
the structure function exponent. This is also seen at Nobeyama
(Holdaway, Ishiguro, and Morita 1995), where the instrumental function
is smaller and the atmospheric phase fluctuations are larger.
Exponents intermediate between the Kolmogorov values of 0.83 for a
thick atmosphere and 0.33 for a thin atmosphere can be obtained from a
superposition of a thick and a thin layer. Hence during the very good
conditions in Chile, most of the turbulent water vapor seems to be in
a thin (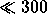 m) layer. This may be the boundary of the inversion
layer that often forms 500-1000 m above that site. In the
distribution of
m) layer. This may be the boundary of the inversion
layer that often forms 500-1000 m above that site. In the
distribution of  (Figure
(Figure  and the relationship between
and the relationship between  and rms
phase suggest there is an everpresent thin turbulent water vapor
layer and a thick turbulent water vapor layer of variable strength that
dominates the phase in all but the best conditions.
and rms
phase suggest there is an everpresent thin turbulent water vapor
layer and a thick turbulent water vapor layer of variable strength that
dominates the phase in all but the best conditions.
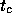 ,
analogous to Masson's (1993) corner frequency, is the time scale
where the phase structure function turns over. We determine it
iteratively: we fit a power law to the temporal phase structure
function between 2 and 15 s time scales and find the mean phase
between 50 and 300 second time scales. Unlike the power spectrum, the
temporal phase structure function is (approximately) flat at long
times. The time where the two fits intersect determines the new upper
limit for the power law fit to the short time scales and the new lower
limit for the mean of the long time scales. This process usually
converges in three iterations. The corner time can be related to the
crossing time of the array, and hence to the velocity, by atmospheric
simulations (i.e., similar to Holdaway, Ishiguro, and Morita 1995).
Simulations of atmospheres with velocities of 5-20 m
,
analogous to Masson's (1993) corner frequency, is the time scale
where the phase structure function turns over. We determine it
iteratively: we fit a power law to the temporal phase structure
function between 2 and 15 s time scales and find the mean phase
between 50 and 300 second time scales. Unlike the power spectrum, the
temporal phase structure function is (approximately) flat at long
times. The time where the two fits intersect determines the new upper
limit for the power law fit to the short time scales and the new lower
limit for the mean of the long time scales. This process usually
converges in three iterations. The corner time can be related to the
crossing time of the array, and hence to the velocity, by atmospheric
simulations (i.e., similar to Holdaway, Ishiguro, and Morita 1995).
Simulations of atmospheres with velocities of 5-20 m 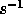 and
structure function exponents of 0.37-0.73 indicate tthe scaling
between
and
structure function exponents of 0.37-0.73 indicate tthe scaling
between 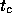 and atmospheric velocity v depends upon the
structure function exponent,
and atmospheric velocity v depends upon the
structure function exponent,

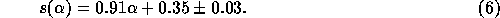


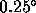 rms white noise is subtracted (filled
squares). The sloping line is the fit to the atmospheric
fluctuations and has a slope of
rms white noise is subtracted (filled
squares). The sloping line is the fit to the atmospheric
fluctuations and has a slope of  . The intersection of the
two lines defines the ``corner time''
. The intersection of the
two lines defines the ``corner time'' 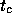 . The oscillations on
long times are probably an indication of the atmospheric velocity,
but we have not yet exploited this information.
. The oscillations on
long times are probably an indication of the atmospheric velocity,
but we have not yet exploited this information.
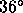 , so zenith
fluctuations would be about 1.3 times lower.
, so zenith
fluctuations would be about 1.3 times lower.
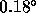 white noise has been subtracted, and the dashed curve is
without calibration.
white noise has been subtracted, and the dashed curve is
without calibration.
 plotted against the rms phase
(a) prior to removing the instrumental
term, and (b) after variance subtraction of a
plotted against the rms phase
(a) prior to removing the instrumental
term, and (b) after variance subtraction of a 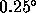 white noise.
Data for 1995 May 10-26 on the Chile site.
white noise.
Data for 1995 May 10-26 on the Chile site.
 for 1995 May 10-26 on the Chile site.
for 1995 May 10-26 on the Chile site.